Lecture 3
Logistic Regression
Logistic Regression
Roadmap
Concepts: what logistic regression is and how classification is evaluated
R coding labs: fitting models, average marginal effects, predicting probabilities, tuning thresholds, and reporting results
By the end of this mini-unit, you should be able to:
- explain why logistic regression is used for binary outcomes
- connect probability ↔︎ odds ↔︎ log-odds (logit)
- describe estimation at a high level (likelihood and deviance)
- compare models using AIC and BIC
- convert predicted probabilities into a classifier using a threshold
- evaluate classification using confusion matrix, precision, recall, specificity, and ROC/AUC
- recognize common issues: class imbalance and (quasi-)separation
Motivation: binary outcomes
Many problems are naturally yes/no (0/1):
- Will a flight be delayed?
- Will a customer churn?
- Is a newborn “at-risk”?
We want:
- Relationship: how predictors change the probability of the outcome
- Prediction (Classfication): a model that produces useful predicted probabilities
Logistic Regression Model
Let the linear combination of predictors be
\[ z_i = \beta_0 + \beta_1 x_{1,i} + \cdots + \beta_k x_{k,i}. \]
Logistic regression models the probability
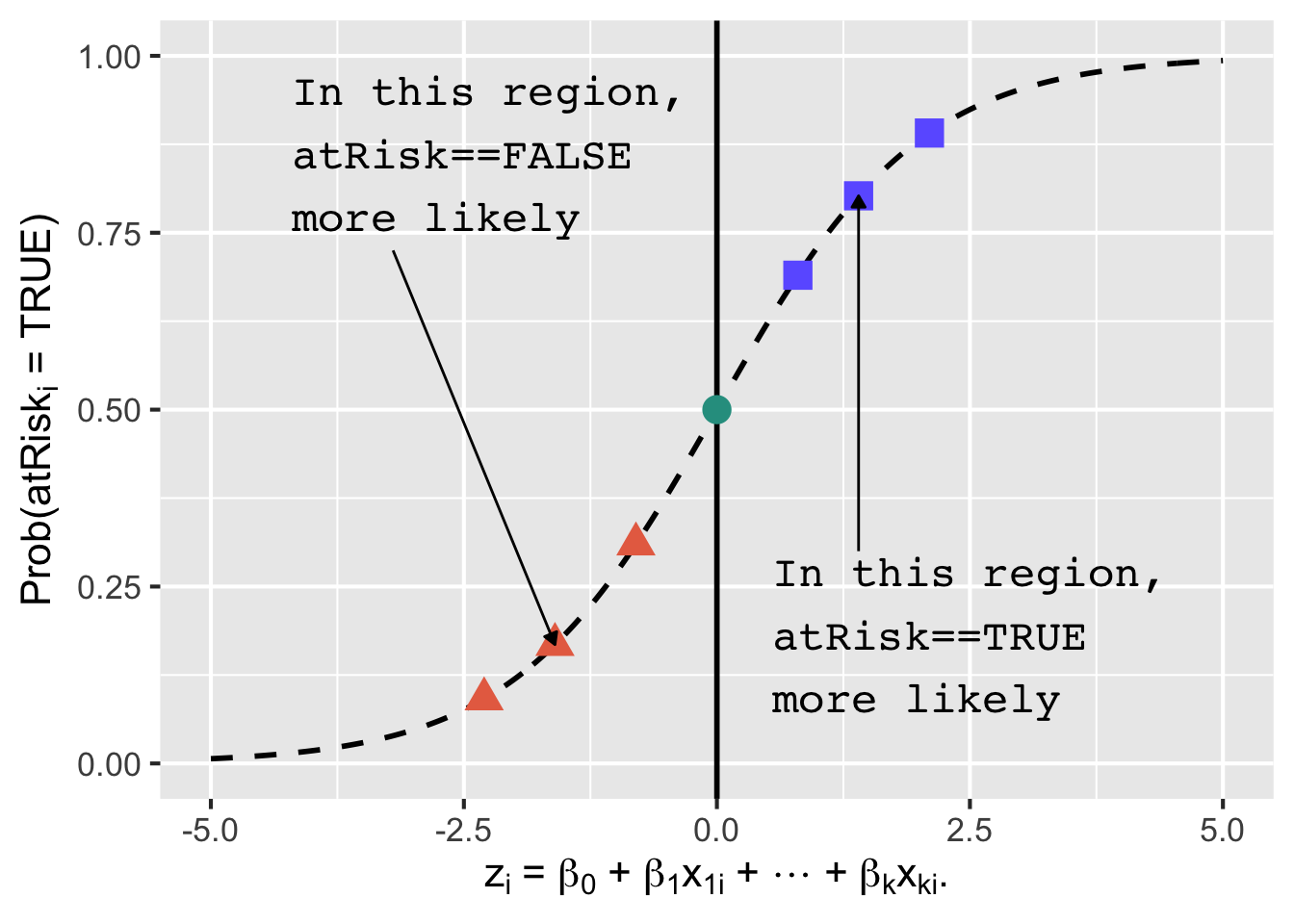
\[ \Pr(y_i = 1 \mid x_i) = G(z_i) = \frac{\exp(z_i)}{1 + \exp(z_i)}. \] That is, the logistic function \(G(z_i)\) maps the linear combination of predictors to the probability that the outcome \(y_{i}\) is \(1\):
\[ z_{i} \rightarrow \Pr(y_i = 1 \mid x_i). \]
Logistic Function
Properties of the Logistic Function
- Range: for any real number \(z\), \(G(z) \in (0,1)\)
- Monotone: larger \(z\) → larger probability
- S-shaped: the “same” change in \(z\) has different impact depending on where you are on the curve
Interpretation:
- \(z_i\) is the model’s score (unbounded)
- \(G(z_i)\) is the predicted probability (bounded)
What is the Logistic Regression doing?
- The logistic regression finds the beta coefficients, \(b_0\), \(b_1\), \(b_2\), \(\cdots\), \(b_{k}\) such that the logistic function \[ G(b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i}) \] is the best possible estimate of the binary outcome \(y_{i}\).
What is the Logistic Regression doing?
The function \(G(z_i)\) is called the logistic function because the function \(G(z_i)\) is the inverse function of a logit (or a log-odd) of the probability that the outcome \(y_{i}\) is 1. \[ \begin{align} G^{-1}(z_i) &\,\equiv\, \text{logit} (\text{Prob}(y_{i} = 1))\\ &\,\equiv \log\left(\, \frac{\text{Prob}(y_{i} = 1)}{\text{Prob}(y_{i} = 0)} \,\right)\\ &\,=\, b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i} \end{align} \]
Logistic regression is a linear regression model for log odds.
Likelihood
Deviance and Likelihood
- Deviance is a measure of the distance between the data and the estimated model.
\[ \text{Deviance} = -2 \log(\text{Likelihood}) + C, \] where \(C\) is constant that we can ignore.
Deviance and Likelihood
- Logistic regression finds the beta coefficients, \(b_0, b_1, \,\cdots, b_k\) , such that the logistic function
\[ G(b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i}) \]
is the best possible estimate of the binary outcome \(y_i\).
Logistic regression finds the beta parameters that maximize the log likelihood of the data, given the model, which is equivalent to minimizing the sum of the residual deviances.
- When you minimize the deviance, you are fitting the parameters to make the model and data look as close as possible.
Likelihood Function
- Likelihood is the probability of your data given the model.
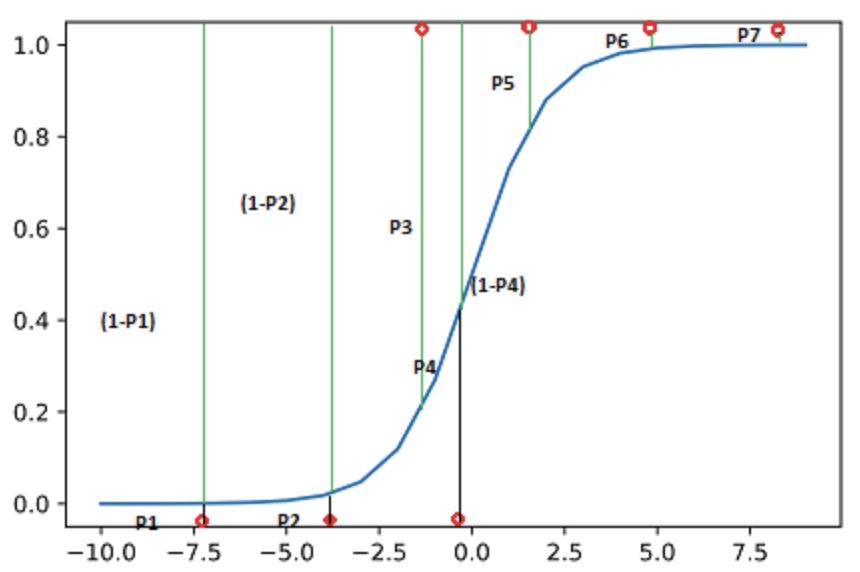
- The probability that the seven data points would be observed:
- \(L = (1-P1)\times(1-P2)\times P3 \times (1-P4) \times P5 \times P6 \times P7\)
- The log of the likelihood: \[ \begin{align} \log(L) &= \log(1-P1) + \log(1-P2) + \log(P3) \\ &\quad+ \log(1-P4) + \log(P5) + \log(P6) + \log(P7) \end{align} \]
AIC and BIC (Model Selection Intuition)
\[ \text{AIC} = -2\,\log L + 2k \qquad\qquad \text{BIC} = -2\,\log L + k\log(n) \]
- AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) help you compare candidate models fit to the same outcome on the same dataset.
- They answer a practical question:
“Is the improvement in fit worth the extra complexity?”
- Both start from the badness-of-fit term: \(-2\log(L)\)
- Smaller AIC/BIC means the model explains the data better.
- Then they add a penalty for estimating more parameters (\(k\)):
- More parameters → more flexibility → higher risk of overfitting.
Marginal Effects
Interpreting Beta Coefficients
- Logistic regression can be expressed as linear regression of log odds of \(y_{i} = 1\) on predictors \(x_1, x_2, \cdots, x_k\):
\[ \begin{align} \text{Prob}(y_{i} = 1) &\,=\, G( b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i} )\\ \text{ }\\ \Leftrightarrow\qquad \log\left(\dfrac{\text{Prob}( y_i = 1 )}{\text{Prob}( y_i = 0 )}\right) &\,=\, b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i} \end{align} \]
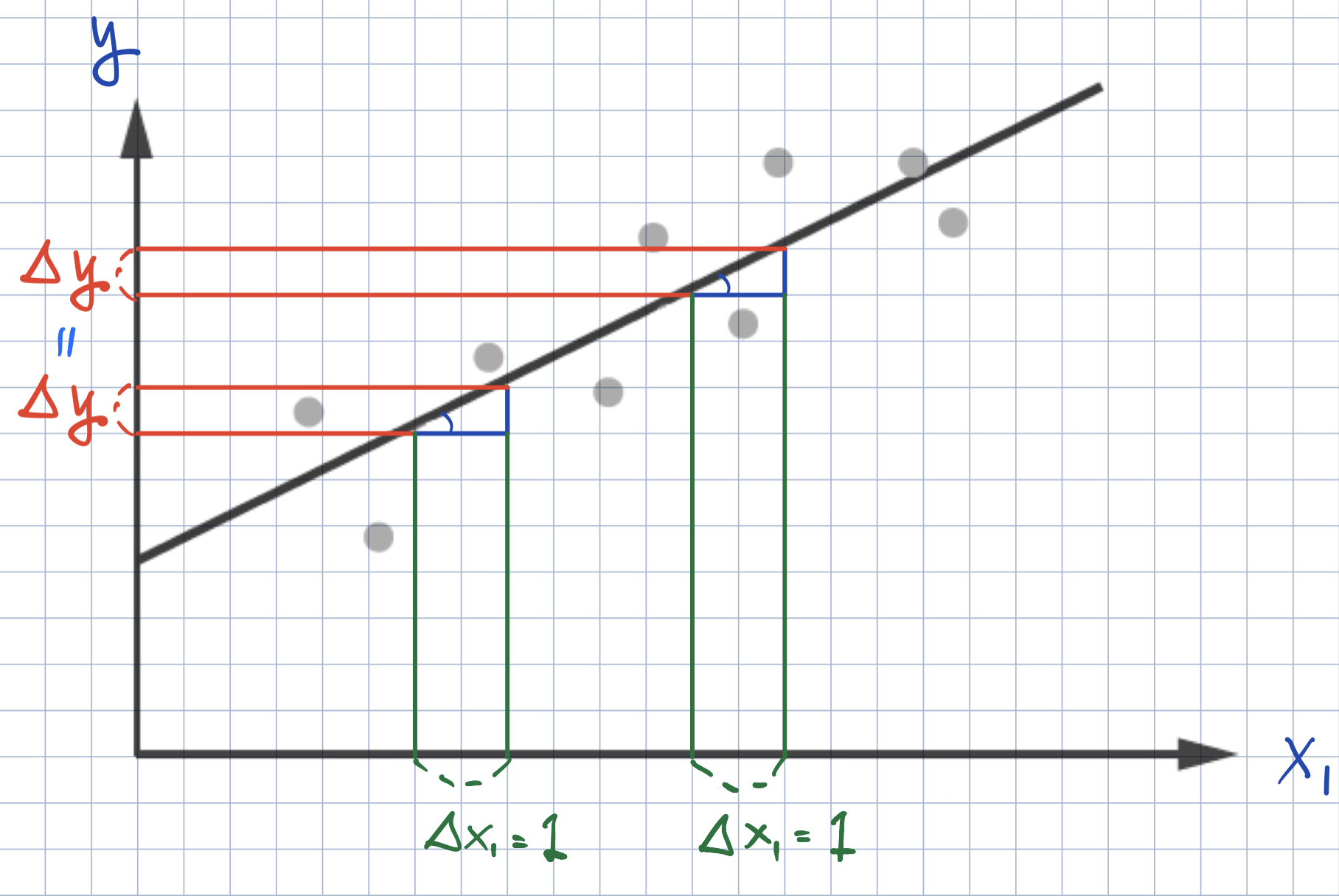
A one-unit increase in \(x_k\) changes the log-odds by \(\beta_k\).
For a binary predictor, it’s relative to the reference category.
Marginal Effects
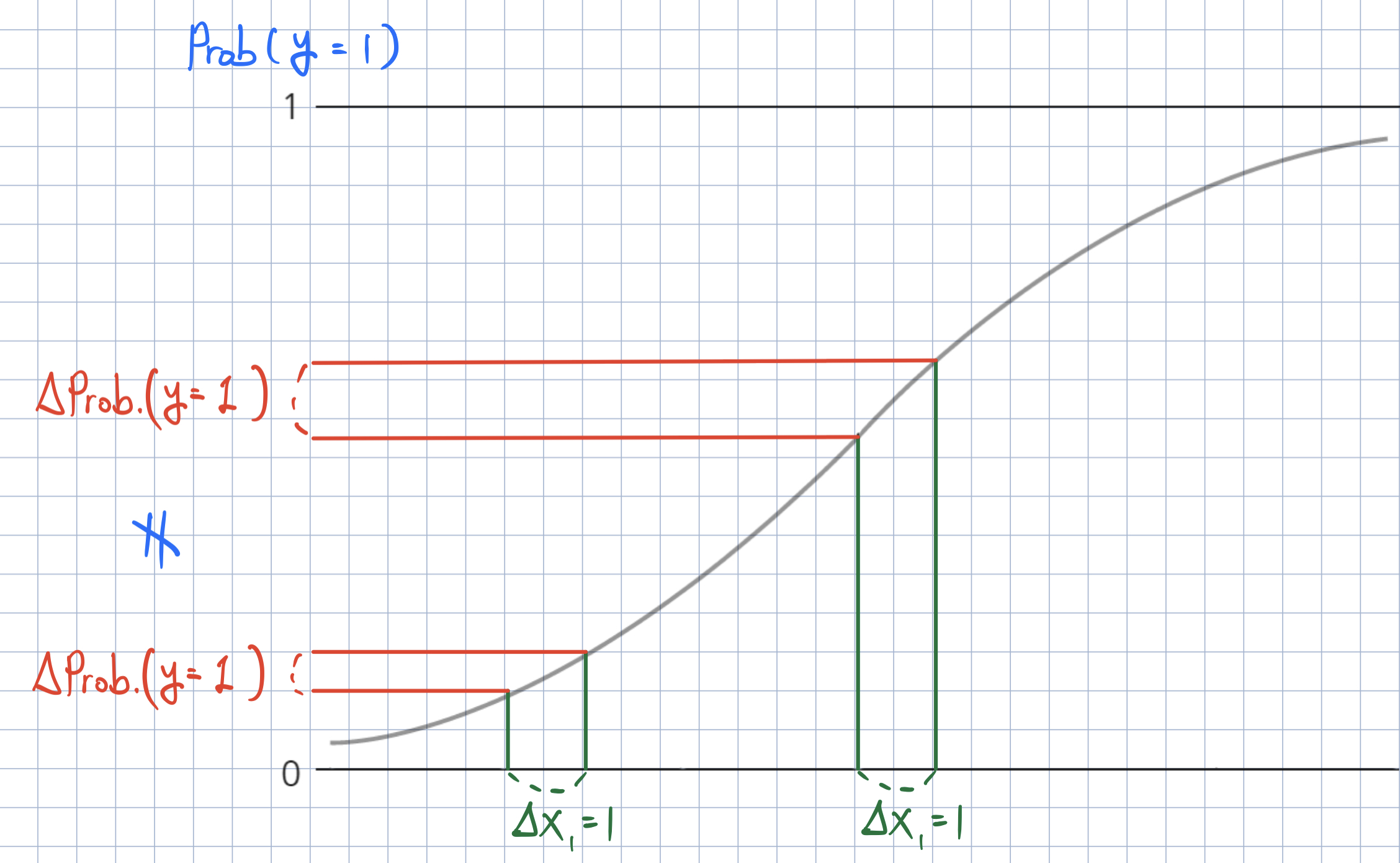
In logistic regression, the coefficient \(\beta_k\) is not a constant change in probability but the log-odds.
The marginal effect on the probability depends on \(z_i\):
\[ \frac{\partial p_i}{\partial x_{k,i}} = \beta_k \; p_i (1-p_i). \]
So the same \(\beta_k\) can imply different probability changes for different observations.
Marginal Effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\)
- In logistic regression, the effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\) is different for each observation \(i\).
Marginal Effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\)
- How can we calculate the effect of \(x_{k, i}\) on the probability of \(y_{i} = 1\)?
- MEM (marginal effect at the mean): compute ME at a “typical” case
- AME (average marginal effect): average the ME across observations
- MEM (marginal effect at the mean): compute ME at a “typical” case
% vs. % point
- Let’s say you have money in a savings account. The interest is 3%.
- Now consider two scenarios:
- The bank increases the interest rate by one percent.
- The bank increases the interest rate by one percentage point.
- What is the new interest rate in each scenario? Which is better?
Classification
Classifier
- Your goal is to use the logistic regression model to classify newborn babies into one of two categories—at-risk or not.
- Prediction from the logistic regression with a threshold on the predicted probabilities can be used as a classifier.
- If the predicted probability that the baby \(\texttt{i}\) is at risk is greater than the threshold, the baby \(\texttt{i}\) is classified as at-risk.
- Otherwise, the baby \(\texttt{i}\) is classified as not-at-risk.
- Double density plot is useful when picking the classifier threshold.
- Since the classifier is built using the training data, the threshold should also be selected using the training data.
Accuracy
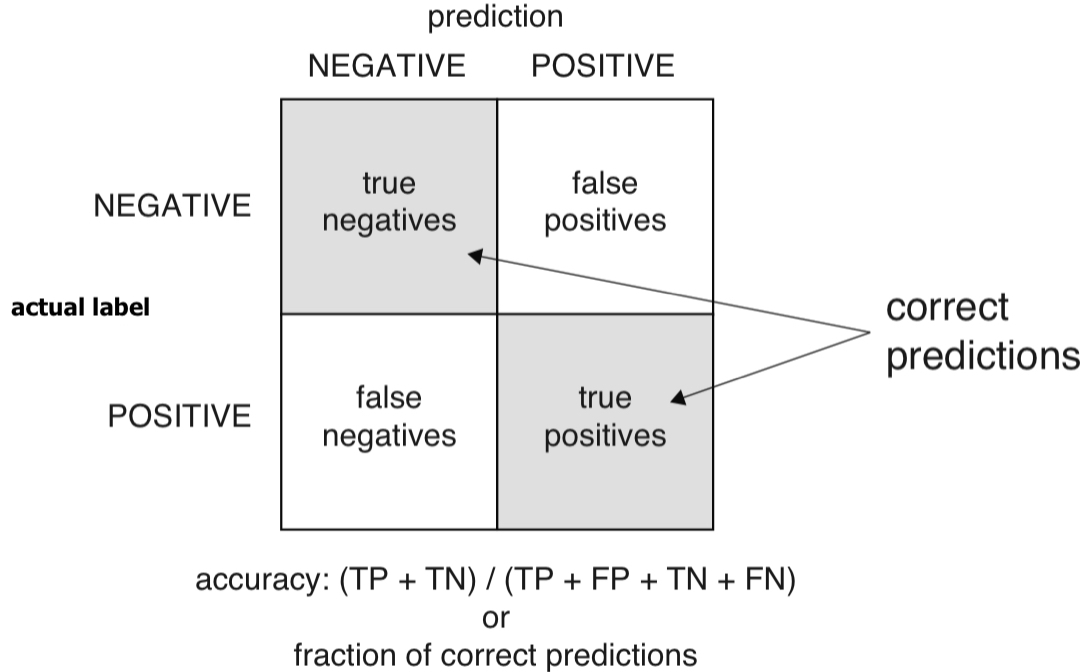
- Accuracy: When the classifier says this newborn baby is at risk or is not at risk, what is the probability that the model is correct?
- Accuracy is defined as the number of items categorized correctly divided by the total number of items.
False positive/negative
- False positive rate (FPR): If the classifier says this newborn baby is at risk, what’s the probability that the baby is not really at risk?
- FPR is defined as the ratio of false positives to predicted positives.
- False negative rate (FNR): If the classifier says this newborn baby is not at risk, what’s the probability that the baby is really at risk?
- FNR is defined as the ratio of false negatives to predicted negatives.
Precision
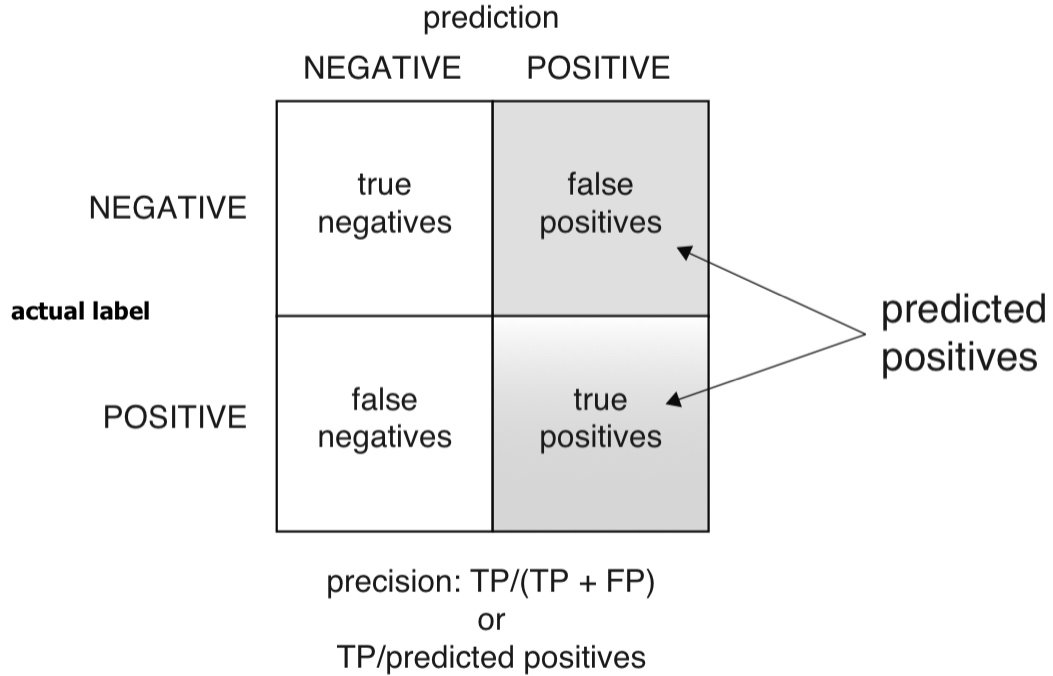
- Precision: If the classifier says this newborn baby is at risk, what’s the probability that the baby is really at risk?
- Precision is defined as the ratio of true positives to predicted positives.
Recall (or Sensitivity)
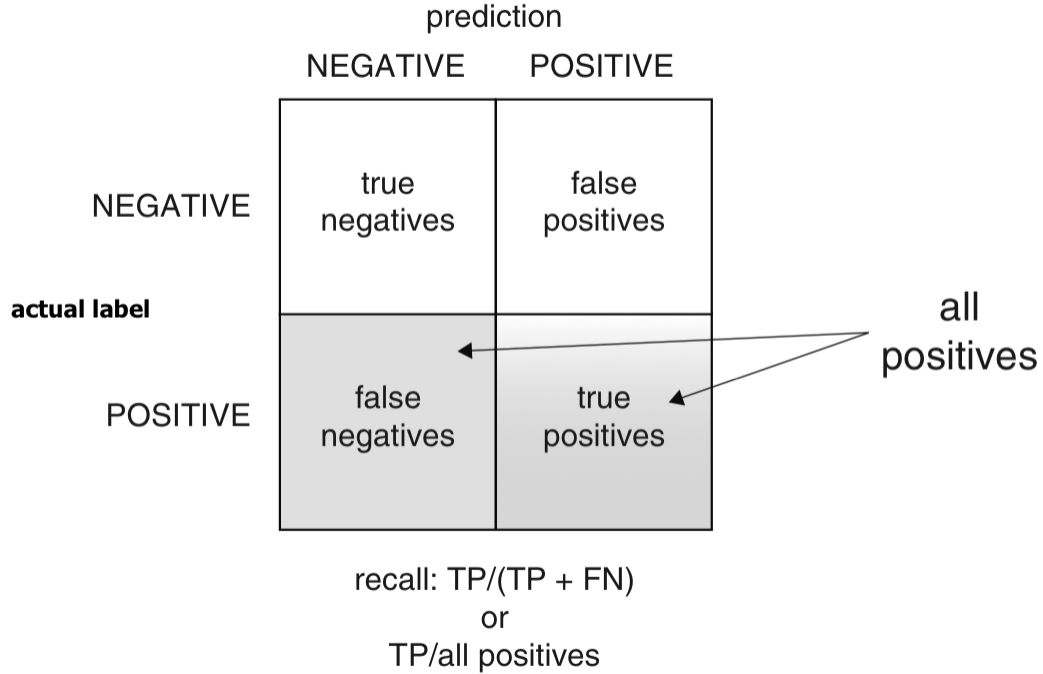
- Recall (or sensitivity): Of all the babies at risk, what fraction did the classifier detect?
- Recall (or sensitivity) is also called the true positive rate (TPR), the ratio of true positives over all actual positives.
Specificity
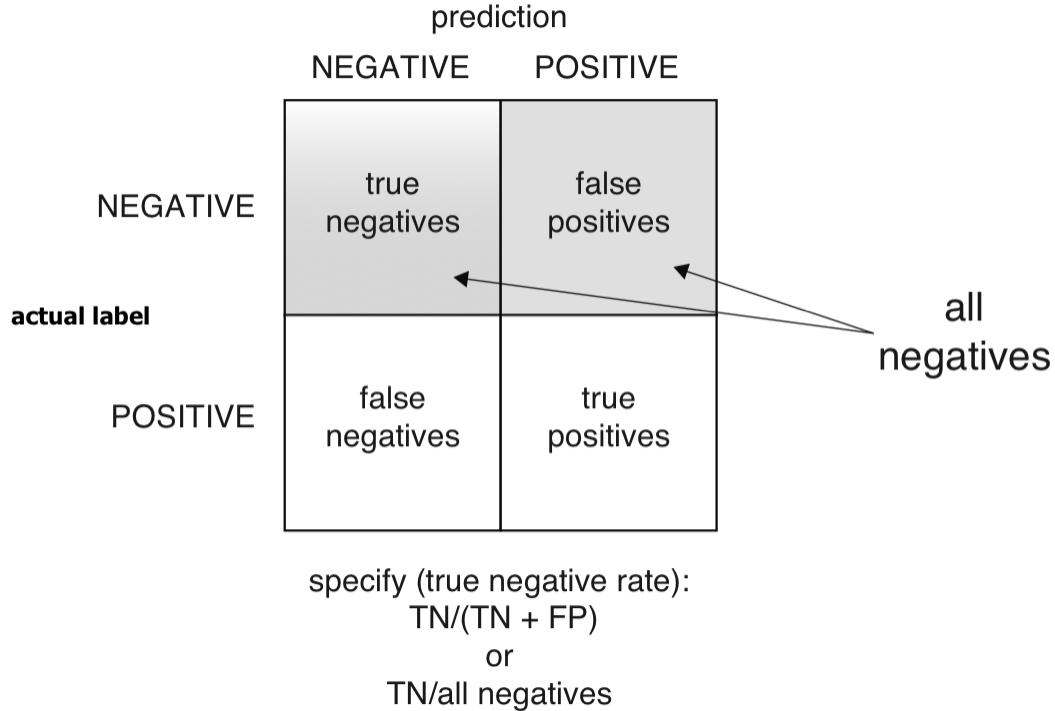
- Specificity: Of all the not-at-risk babies, what fraction did the classifier detect?
- Specificity is also called the true negative rate (TNR), the ratio of true negatives over all actual negatives.
Enrichment
- Average: Average rate of new born babies being at risk
- Enrichment: How does the classifier precisely choose babies at risk relative to the average rate of new born babies being at risk?
- We want a classifier whose enrichment is greater than 2.
- There is a trade-off between recall and precision/enrichment.
- There is also a trade-off between recall and specificity.
- What would be the optimal threshold?
ROC and AUC
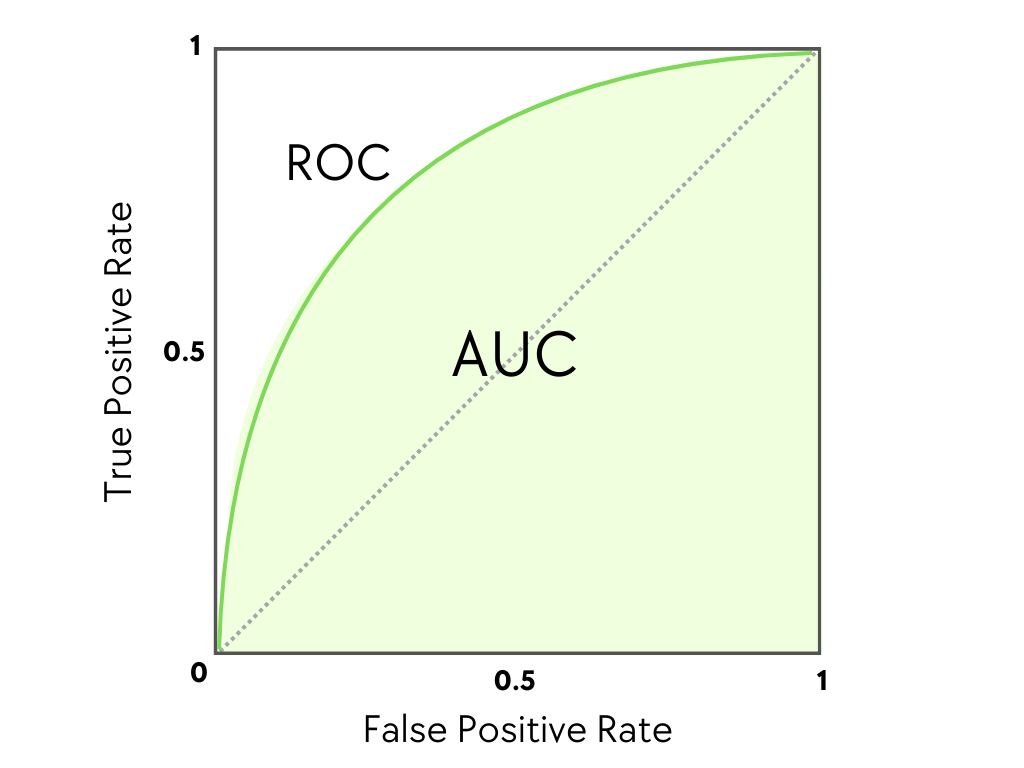
The receiver operating characteristic curve (or ROC curve) plots both the true positive rate (recall) and the false positive rate (or 1 - specificity) for all threshold levels.
- Area under the curve (or AUC) can be another measure of the quality of the model.
ROC - (0,0)
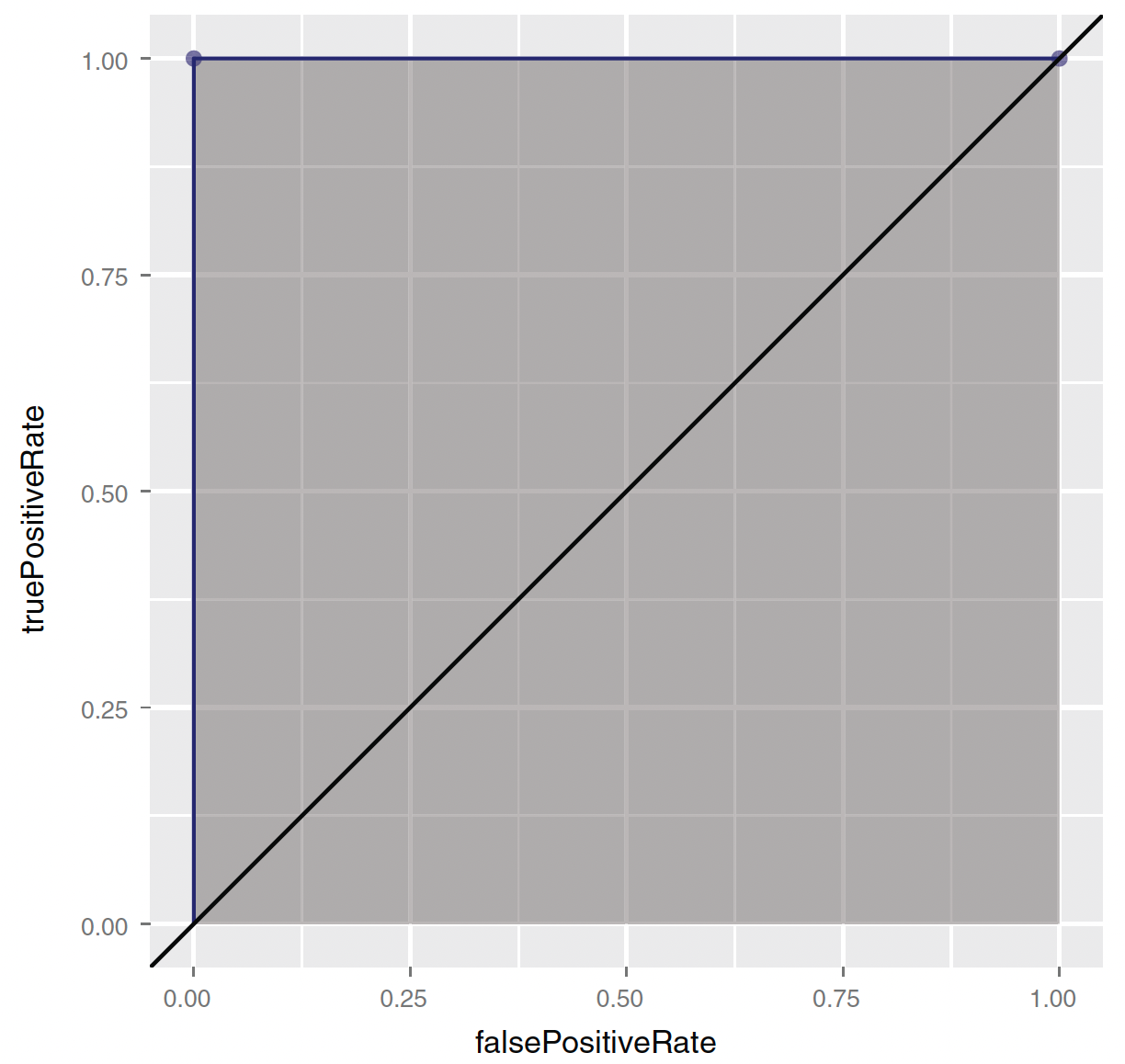
- (0,0)—Corresponding to a classifier defined by the threshold \(\text{Prob}(y_{i} = 1) = 1\):
- Nothing gets classified as at-risk.
ROC - (1,1)

- (1,1)—Corresponding to a classifier defined by the threshold \(\text{Prob}(y_{i} = 1) = 0\):
- Everything gets classified as at-risk.
ROC - (0,1)

- (0,1)—Corresponding to any classifier defined by a threshold between 0 and 1:
- Everything is classified perfectly!
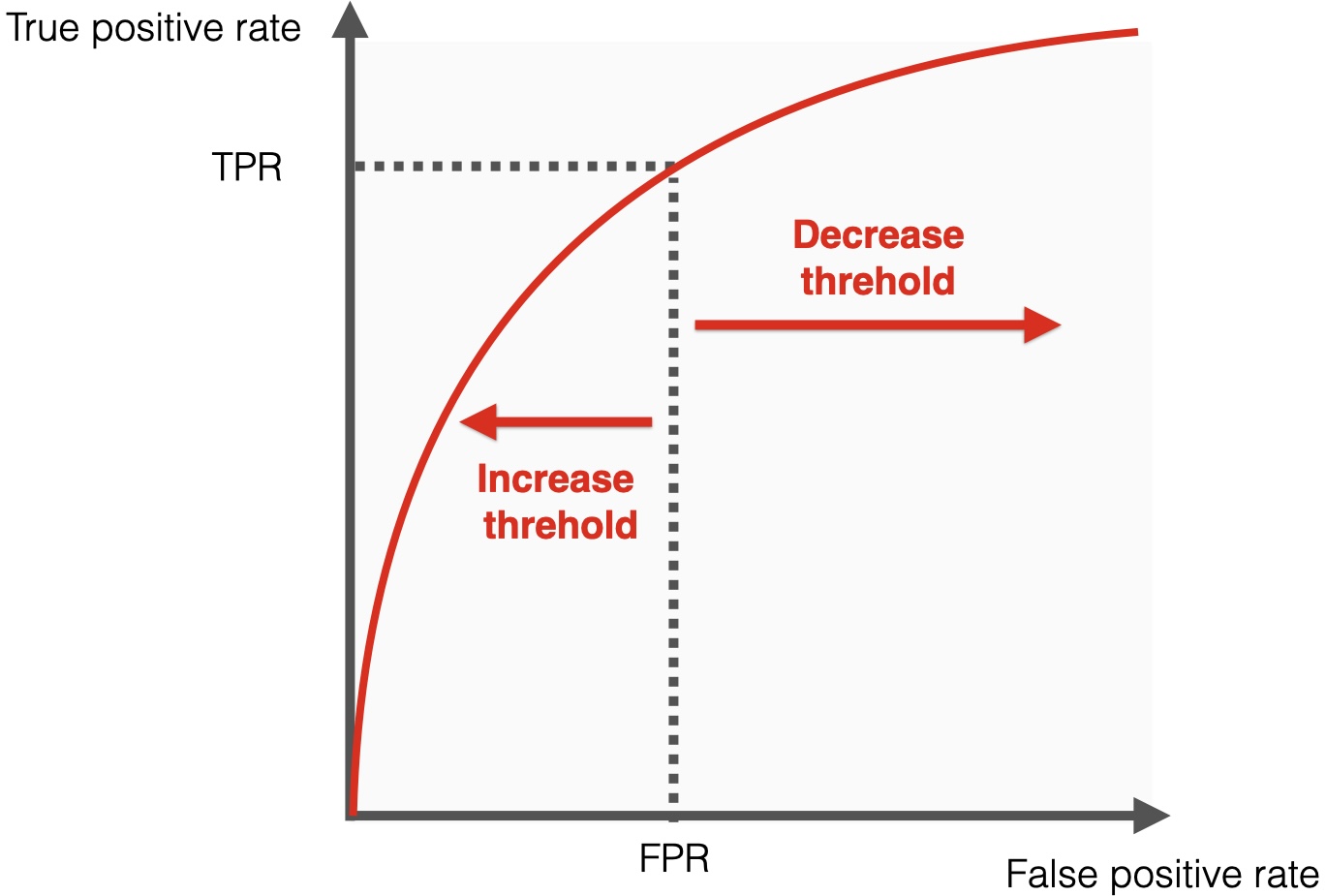
ROC and Thresholds
AUC
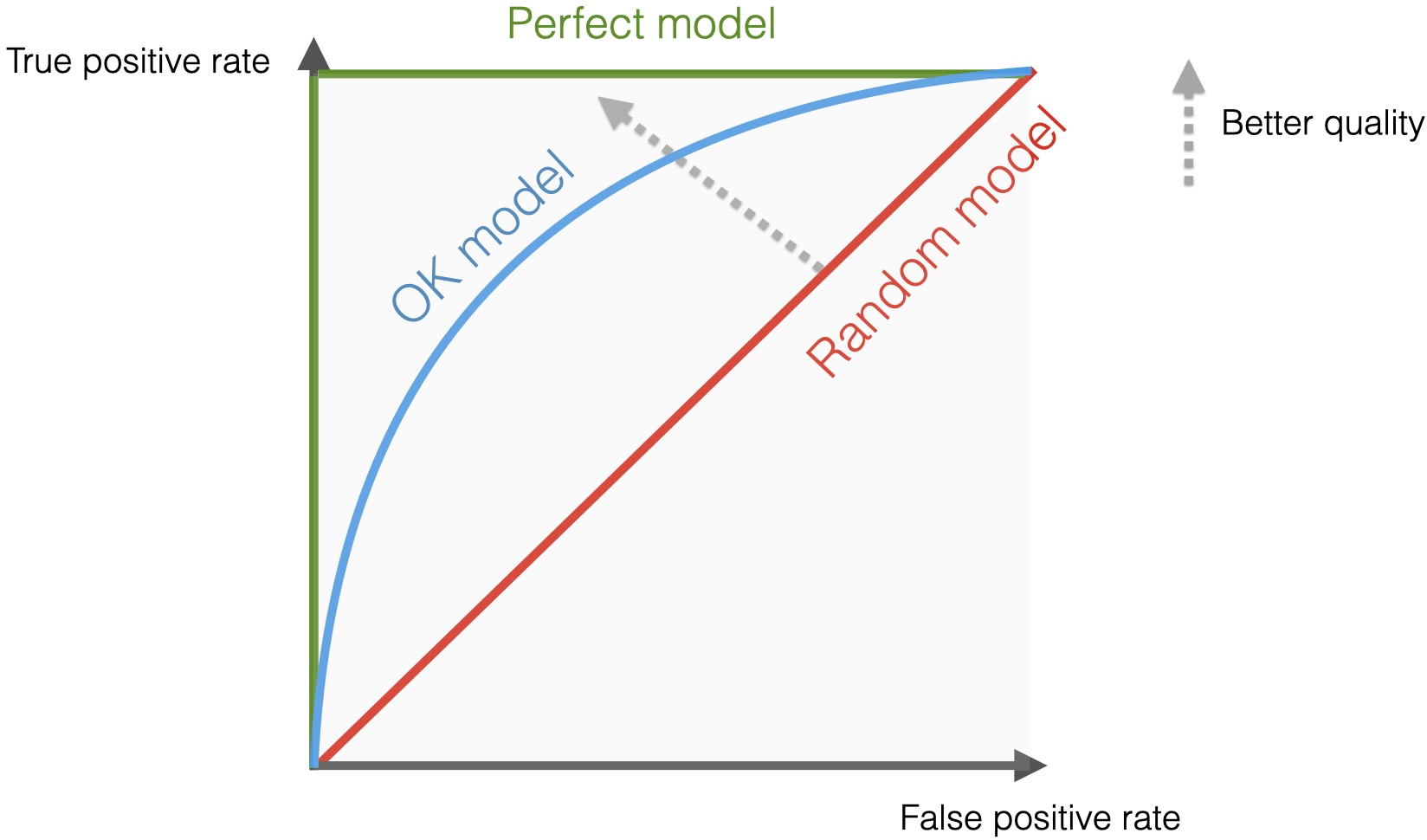
- AUC measures overall performance across all thresholds, with 1.0 being perfect.
Performance of Classifier
- Which classifier do you prefer for identifying at-risk babies?
- High accuracy, low recall, other things being equal;
- Low accuracy, high recall, other things being equal.
- Accuracy may not be a good measure for the classes that have unbalanced distribution of predicted probabilities (e.g., rare event).
Accuracy Can Be Misleading in Imbalanced Data
- Rare events (e.g., severe childbirth complications) occur in a very small percentage of cases (e.g., 1% of the population).
- A simple model that always predicts “not-at-risk” would be 99% accurate, as it correctly classifies 99% of cases where no complications occur.
- However, this does not mean the simple model is better—accuracy alone does not capture the effectiveness of a model when class distributions are skewed.
- A better model that identifies 5% of cases as “at-risk” and catches all true at-risk cases may appear to have lower overall accuracy than the simple model.
- Missing a severe complication (false negative) can be more costly than mistakenly flagging a healthy case as at risk (false positive).
Separation and Quasi-separation
What is Separation?
- One of the model variables or some combination of the model variables predicts the outcome perfectly for at least a subset of the training data.
- You’d think this would be a good thing; but, ironically, logistic regression fails when the variables are too powerful.
- Separation occurs when a predictor (or combination of predictors) perfectly separates the outcome classes.
- For example, if:
- All
fail = TRUEwhensafety = low, and - All
fail = FALSEwhensafety ≠ low,
then the model can predict the outcome with 100% accuracy based onsafety.
- All
- ➡️ This leads to infinite (non-estimable) coefficients.
What is Quasi-Separation?
- Quasi-separation occurs when:
- Some, but not all, values of a predictor perfectly predict the outcome.
- Example:
fail = TRUEfor all cars withsafety = low,
- But
failis mixed forsafety = medorhigh.
- ➡️ Model still suffers from unstable coefficient estimates or high standard errors.