Lecture 9

Data Visualization

Byeong-Hak Choe

bchoe@geneseo.edu

SUNY Geneseo

November 3, 2025

Data Visualization

Data Storytelling

→

📊💡 Data-Driven Insights

• Data storytelling bridges the gap between data and insight by integrating descriptive statistics, data transformation, visualization, and narration within the appropriate audience context to communicate findings effectively and support data-informed decision-making.

Data Storytelling - Visualization

• Data Visualization: Convert data into meaningful graphics for better understanding of data.

• There are many different graphs and other types of visual displays of information.

We will visualize:

• The distribution of a categorical variable
• The distribution of a numeric variable

• The relationship between two numeric variables
• The time trend of a numeric variable

Distribution

Distribution and Variation

Distribution

• Distribution describes how the values of a variable are spread or grouped within a dataset (data.frame).
  • It reveals the overall pattern of how observations differ or cluster.
    
  • Understanding distribution helps us see where data are concentrated and where they are sparse.

Variation

• Variation is the tendency of a variable’s values to differ from one measurement to another.
  • In everyday life, we observe variation everywhere — measuring the same numeric variable twice often gives slightly different results.
    
  • Recognizing variation helps us understand change and spread in data.

✨ Together, distribution and variation form the foundation of data analysis.

🔍 Key Questions When Analyzing Distribution

• Which values are most common, and why?

• Which values are rare, and why?
  → Does this pattern align with your expectations, or reveal something surprising?

• How wide is the spread?
  → Are the values tightly clustered or widely dispersed? (e.g., range, IQR, standard deviation)

• Are there any outliers?
  → What causes them — data errors, unusual events, or genuine variation?

• What is the shape of the distribution?
  → Is it symmetric, skewed, unimodal, or bimodal?

• Are there patterns or subgroups?
  → Do certain categories or conditions show different distributions?

Distribution

• How you visualize the distribution of a variable depends on the type of variable: categorical or numerical.

• Categorical Variables: Represent categories or groups (e.g., colors, departments, types)
  • Common visualizations:
    Bar charts
  • Example: Distribution of favorite sports among students

• Numerical Variables: Represent numbers with meaningful values (e.g., age, income, temperature)
  • Common visualizations: Histograms, Box plots
  • Example: Distribution of heights in a class

Titanic Data

Bar Chart

Horizontal Bar Chart

Stacked Bar Chart

100% Stacked Bar Chart

Clustered Bar Chart

Histogram

Histogram

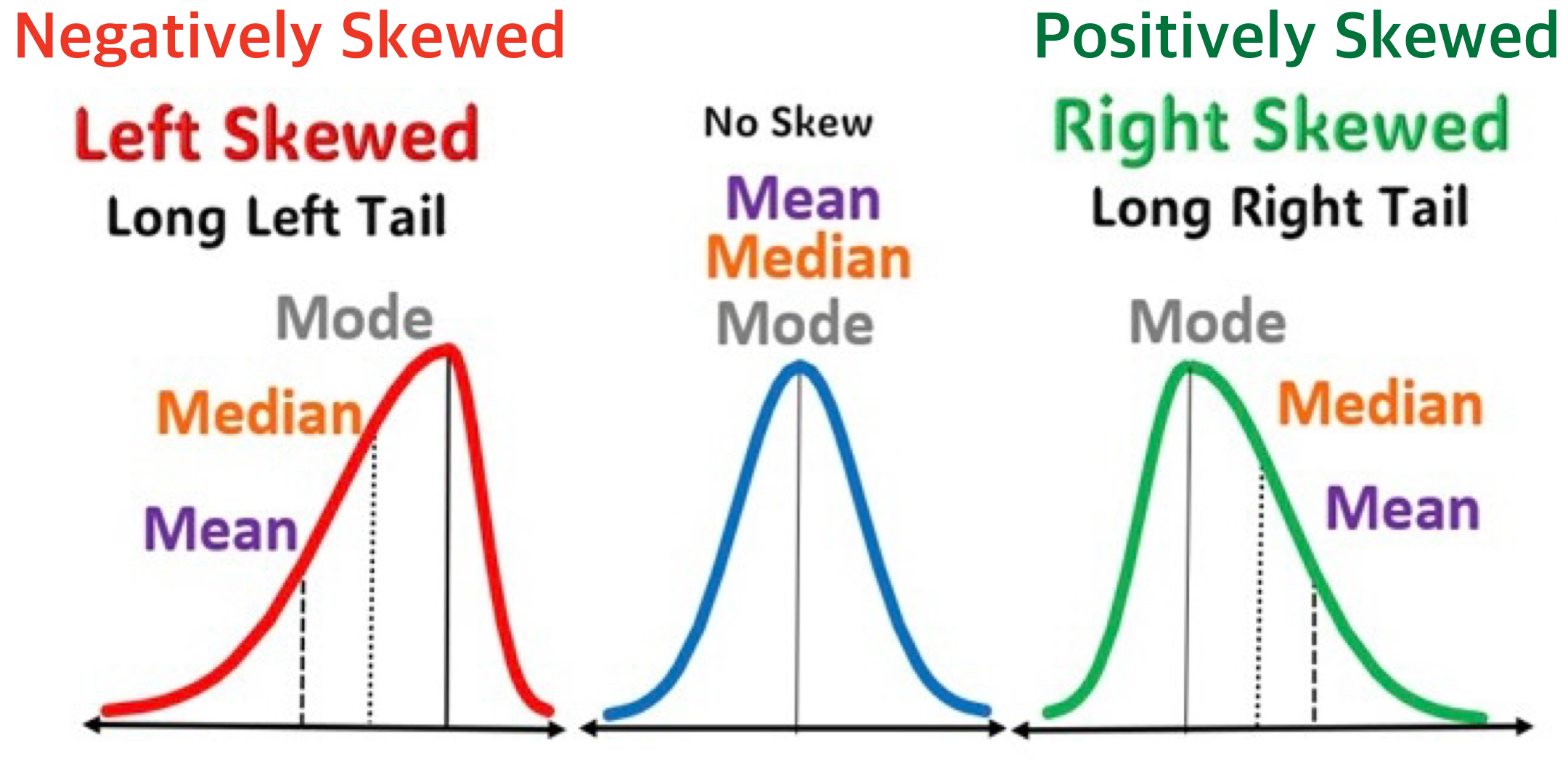
⚖️ Skewness

• In a distribution, skewness describes the asymmetry of a distribution.
  • It shows whether the data are stretched more to the left or right of the center.

🏔️ Modality

• How many peaks does the distribution have?
  • Is it unimodal (one peak) or bimodal (two peaks)?
    
  • Or perhaps uniform or multimodal?

Boxplot

Relationship

🔗 Relationship

• When examining plots with two numeric variables, we look for co-variation — the tendency of two variables to change together in a related way.

• 🔍 Key questions to ask:

  • Are the variables positively related (as one increases, the other increases)?
  • Are they negatively related (as one increases, the other decreases)?
  • Or is there no clear relationship between them?

• Common visualizations:

  • Scatterplot
  • Fitted line or curve to reveal the pattern of association

Orange Juice Sales

Scatterplot

Scatterplot with Fitted Line

Scatterplot with Fitted Line

MPG Data

Scatterplot with Fitted Line

Weather Data

Scatterplot with Fitted Line

⚙️ Input vs. Outcome: Plotting Relationships

• Be mindful of how you place variables on the axes.

  • It’s standard practice to put the input variable on the x-axis and the outcome variable on the y-axis.

• Input Variable → represents the potential cause or influencing factor.
  

• Outcome Variable → represents the potential effect or result.

  • Example: Advertising budget (input) vs. sales revenue (outcome)

Correlation Does Not Imply Causation

• Just because you uncover a relationship doesn’t mean you’ve identified the “causal” relationship.

⚠️ Correlation ≠ Causation

• Caution: A strong correlation between two variables does not mean that one causes the other to change.
  • Two variables can move together by coincidence or due to a third, unseen factor.
• Correlation describes the strength and direction of a linear relationship between two variables:
  • Positive / Negative → direction of relationship
    
  • Strong / Weak → how clear (or uncertain) the relationship is
  • Slope → the rate of change in the outcome per unit of input
• Causation means that one variable directly affects another.
  • Demonstrating causation requires controlled experiments or supporting evidence beyond correlation.
    
  • e.g.,: Smoking causes an increase in lung cancer risk (causation).

Time Trend

⏰ Time Trend

• A time trend (or time series) plot shows how a variable changes over time, revealing trends, patterns, and fluctuations.

  • The x-axis represents time, and the y-axis represents the measured variable.

• It helps us observe the overall direction of change — whether the variable is increasing, decreasing, or remaining relatively stable over time.

• Common visualizations:

  • Line chart
  • Fitted curve to smooth short-term fluctuations

NVDA Stock Price Data

Line Chart

Line Chart with Fitted Curve