Lecture 7

R Basics

Byeong-Hak Choe
bchoe@geneseo.edu

SUNY Geneseo

September 11, 2024

R Basics

R Basics

Functions

  • A function can take any number and type of input parameters and return any number and type of output results.

  • R ships a vast number of built-in functions.

  • R also allows a user to define a new function.

  • We will mostly use built-in functions.

R Basics

Functions, Arguments, and Parameters

library(tidyverse)

# The function `str_c()`, provided by `tidyverse`, concatenates characters.
str_c("Data", "Analytics")
str_c("Data", "Analytics", sep = "!")

  • We invoke a function by entering its name and a pair of opening and closing parentheses.

  • Much as a cooking recipe can accept ingredients, a function invocation can accept inputs called arguments.

  • We pass arguments sequentially inside the parentheses (, separated by commas).

  • A parameter is a name given to an expected function argument.

  • A default argument is a fallback value that R passes to a parameter if the function invocation does not explicitly provide one.

R Basics

Arithmetic Operations and Mathematical Functions

5 + 3
5 - 3
5 * 3
5 / 3
5^3
( 3 + 4 )^2
3 + 4^2
3 + 2 * 4^2
3 + 2 * 4 + 2
(3 + 2) * (4 + 2)

  • All of the basic operators with parentheses we see in mathematics are available to use.

  • R can be used for a wide range of mathematical calculations.

5 * abs(-3)
sqrt(17) / 2
exp(3)
log(3)
log(exp(3))
exp(log(3))
  • R has many built-in mathematical functions that facilitate calculations and data analysis.
  • abs(x): the absolute value \(|x|\)
  • sqrt(x): the square root \(\sqrt{x}\)
  • exp(x): the exponential value \(e^x\), where \(e = 2.718...\)
  • log(x): the natural logarithm \(\log_{e}(x)\), or simply \(\log(x)\)

R Basics

Vectorized Operations

a <- c(1, 2, 3, 4, 5)
b <- c(5, 4, 3, 2, 1)

a + b
a - b
a * b
a / b
sqrt(a)
  • Vectorized operations mean applying a function to every element of a vector without explicitly writing a loop.
    • This is possible because most functions in R are vectorized, meaning they are designed to operate on vectors element-wise.
    • Vectorized operations are a powerful feature of R, enabling efficient and concise code for data analysis and manipulation.

Descriptive Statistics

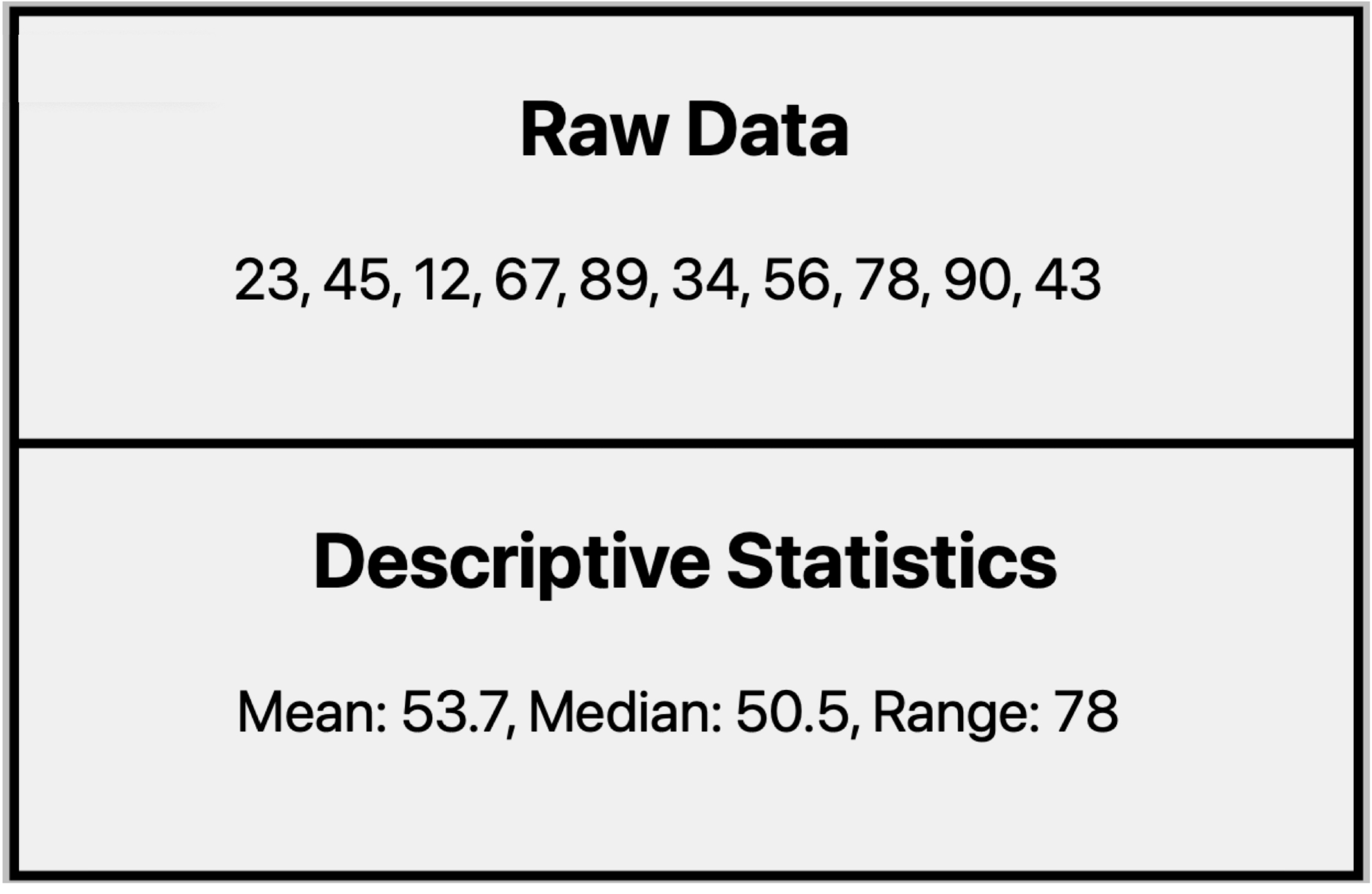
  • Descriptive statistics condense data into manageable summaries, making it easier to understand key characteristics of the data.

    • They help reveal patterns, trends, and relationships within the data that might not be immediately apparent from raw numbers.

Descriptive Statistics

  • Data quality assessment:
    • Descriptive statistics can highlight potential issues in data quality, such as outliers or unexpected distributions, prompting further investigation.
  • Foundation for further analysis:
    • Descriptive statistics often serve as a starting point for more advanced statistical analyses and predictive modeling.
  • Data visualization enhancement:
    • Descriptive statistics often form the basis for effective data visualizations, making complex data more accessible and understandable.

Descriptive Statistics

Measures of Central Tendency

  • Measures of centrality are used to describe the central or typical value in a given vector.
    • They represent the “center” or most representative value of a data set.
  • To describe this centrality, several statistical measures are commonly used:
    • Mean: The arithmetic average of all values in the data set.
    • Median: The middle value when the data set is ordered from least to greatest.
    • Mode: The most frequently occurring value in the data set.

Measures of Central Tendency

Mean

\[ \overline{x} = \frac{x_{1} + x_{2} + \cdots + x_{N}}{N} \]

x <- c(1, 2, 3, 4, 5)
sum(x)
mean(x)
  • The arithmetic mean (or simply mean or average) is the sum of all the values divided by the number of observations in the data set.
    • mean() calculates the mean of the values in a vector.
    • For a given vector \(x\), if we happen to have \(N\) observations \((x_{1}, x_{2}, \cdots , x_{N})\), we can write the arithmetic mean of the data sample as above.

Measures of Central Tendency

Median

x <- c(1, 2, 3, 4, 5)
median(x)
  • The median is the measure of center value in a given vector.
    • median() calculates the median of the values in a vector.

Measures of Central Tendency

Mode

  • The mode is the value(s) that occurs most frequently in a given vector.

  • Mode is useful, although it is often not a very good representation of centrality.

  • The R package, modest, provides the mfw(x) function that calculate the mode of values in vector x.

Descriptive Statistics

Measures of Dispersion

  • Measures of dispersion are used to describe the degree of variation in a given vector.
    • They are a representation of the numerical spread of a given data set.
  • To describe this dispersion, a number of statistical measures are developed
    • Range
    • Variance
    • Standard deviation
    • Quartile

Measures of Dispersion

Range

\[ (\text{range of x}) \,=\, (\text{maximum value in x}) \,-\, (\text{minimum value in x}) \]

x <- c(1, 2, 3, 4, 5)
max(x)
min(x)
range <- max(x) - min(x)
  • The range is the difference between the largest and the smallest values in a given vector.
    • max(x) returns the maximum value of the values in a given vector \(x\).
    • min(x) returns the minimum value of the values in a given vector \(x\).

Measures of Dispersion

Variance

\[ \overline{s}^{2} = \frac{(x_{1}-\overline{x})^{2} + (x_{2}-\overline{x})^{2} + \cdots + (x_{N}-\overline{x})^{2}}{N-1}\;\, \]

x <- c(1, 2, 3, 4, 5)
var(x)
  • The variance is used to calculate the deviation of all data points in a given vector from the mean.
    • The larger the variance, the more the data are spread out from the mean and the more variability one can observe in the data sample.
    • To prevent the offsetting of negative and positive differences, the variance takes into account the square of the distances from the mean.
  • var(x) calculates the variance of the values in a vector \(x\).

Measures of Dispersion

Standard Deviation

\[ \overline{s} = \sqrt{ \left( \frac{(x_{1}-\overline{x})^{2} + (x_{2}-\overline{x})^{2} + \cdots + (x_{N}-\overline{x})^{2}}{N-1}\;\, \right) } \]

x <- c(1, 2, 3, 4, 5)
sd(x)
  • The standard deviation (SD)—the square root of the variance—is also a measure of the spread of values within a given vector.
    • sd(x) calculates the standard deviation of the values in a vector \(x\)
    • SD helps us understand how representative the mean is of the data.
      • A low SD suggests that the mean is a good summary, while a high SD suggests greater variability around the mean.

Measures of Dispersion

Quartiles

quantile(x)
quantile(x, 0) # the minimum
quantile(x, 0.25) # the 1st quartile
quantile(x, 0.5) # the 2nd quartile
quantile(x, 0.75) # the 3rd quartile
quantile(x, 1) # the maximum
  • A quartile is a quarter of the number of data points in a given vector.
    • Quartiles are determined by first sorting the values and then splitting the sorted values into four disjoint smaller data sets.
    • Quartiles are a useful measure of dispersion because they are much less affected by outliers or a skewness in the data set than the equivalent measures in the whole data set.

Measures of Dispersion

Interquartile Range

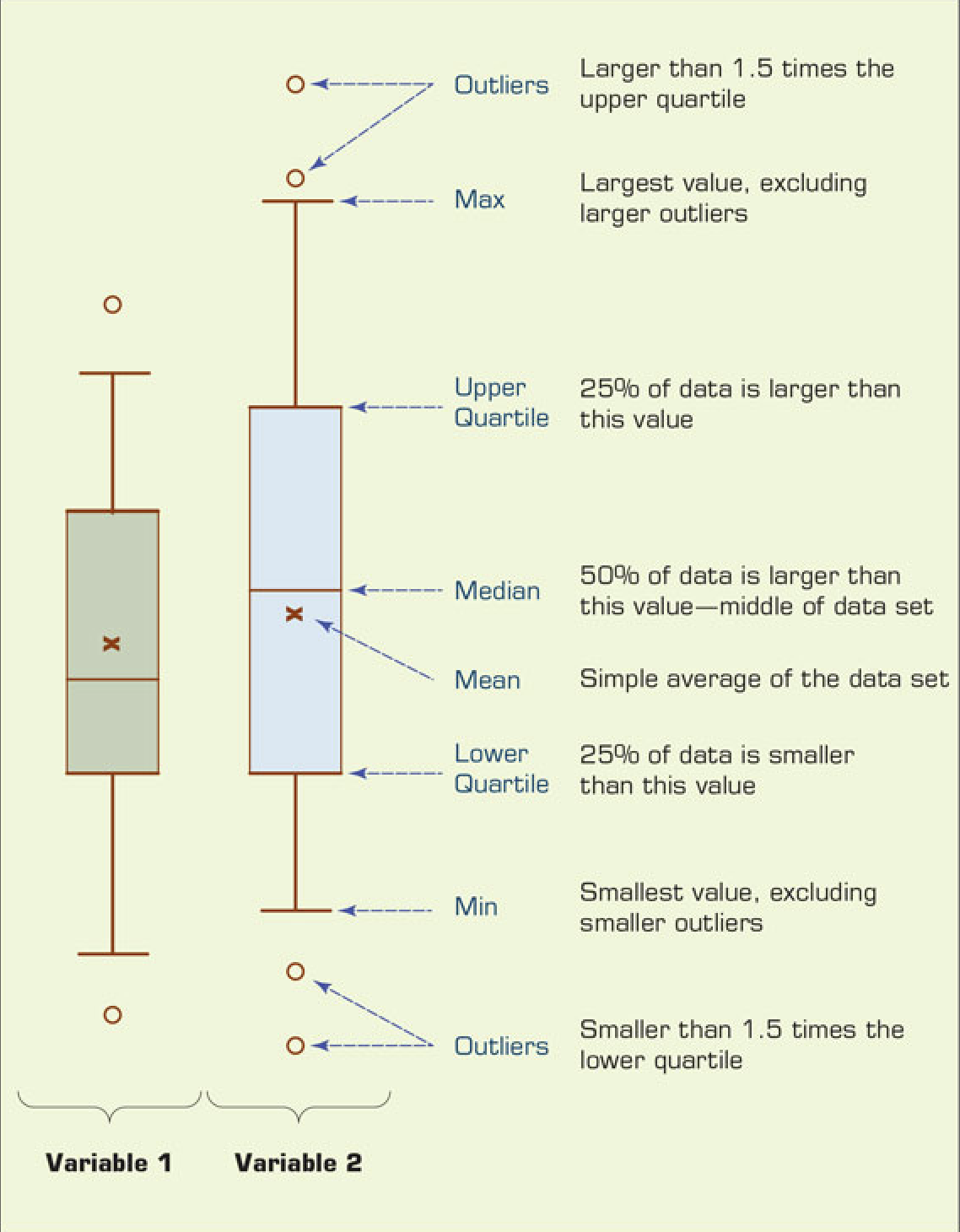
  • An interquartile range describes the difference between the third quartile (Q3) and the first quartile (Q1), telling us about the range of the middle half of the scores in the distribution.
    • The quartile-driven descriptive measures (both centrality and dispersion) are best explained with a popular plot called a box plot.

R Basics

Absolute vs. Relative Pathnames

  • Complete path from the root directory to the target file or directory.

  • Independent of the current working directory.

  • Example

    • Mac:
      • /Users/user/documents/data/car_data.csv
    • Windows:
      • C:\\Users\\user\\Documents\\data\\car_data.csv
  • Path relative to the working directory.
    • Relative path changes based on the working directory.
  • Example:
    • Absolute pathname for car_data.csv is /Users/user/documents/data/car_data.csv.
    • Suppose the current directory is /Users/user/documents/.
    • Then, the relative pathname for car_data.csv is dada/car_data.csv.
  • For the Posit Cloud project, we can use a relative path.
    • The current working directory in is /cloud/project/

R Basics

Working with Data from Files

  • We use the read_csv() function to read a comma-separated values (CSV) file.

  1. Download the CSV file, car_data.csv from the Class Files module in our Brightspace.

  2. Create a sub-directory, data, by clicking “New Folder” in the Files Pane in Posit Cloud.

  3. Upload the car_data.csv file to the sub-directory data.

  4. Provide the relative pathname for the file, car_data.csv, to the read_csv() function.

uciCar <- read_csv('HERE WE PROVIDE A RELATIVE PATHNAME FOR car_data.csv')
View(uciCar)
  • View()/view() displays the data in a simple spreadsheet-like grid.

R Basics

Examining data.frames

class(uciCar)
dim(uciCar)
nrow(uciCar)
ncol(uciCar)
library(skimr)
skim(uciCar)
  • dim() shows how many rows and columns are in the data for data.frame.
  • nrow() and ncol() shows the number of rows and columns for data.frame respectively.
  • skimr::skim() provides a more detailed summary.
    • skimr is the R package that provides the function skim().

R Basics

Reading data.frames from an URL

tvshows <- read_csv(
        'https://bcdanl.github.io/data/tvshows.csv')
  • We can import the CSV file from the web.

R Basics

Tidy data.frame: Variables, Observations, and Values

  • There are three rules which make a data.frame tidy:

    1. Each variable must have its own column.
    2. Each observation must have its own row.
    3. Each value must have its own cell.

:::

–> –> –> –>