Lecture 9

K-fold Cross-Validation; Regularized Regression

Byeong-Hak Choe
bchoe@geneseo.edu

SUNY Geneseo

March 26, 2025

\(K\)-fold Cross-Validation

K-fold Cross-Validation


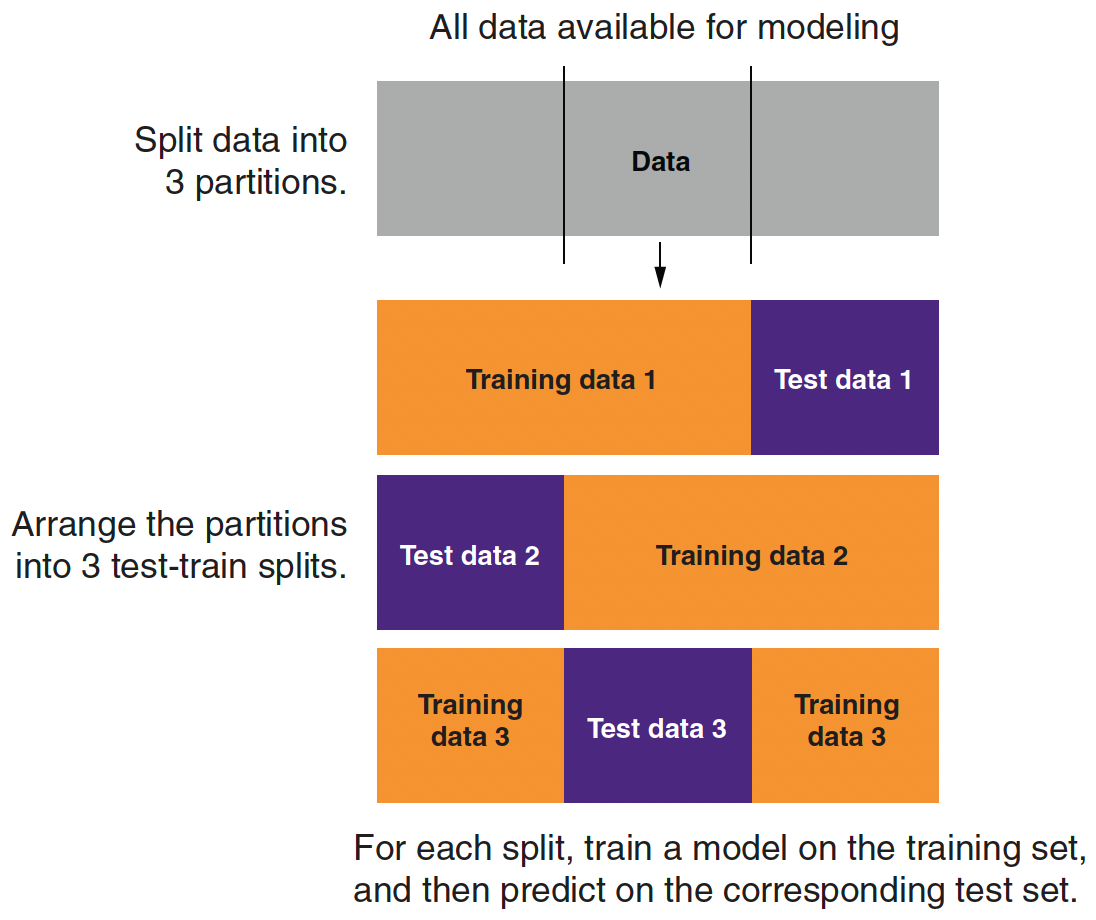
Partitioning Data for 3-fold Cross-Validation

  • A single train–test split uses each subset only once—either for training or for evaluation.
  • K‑fold cross-validation divides the training data into K equal parts (folds).
    • For each fold \(k=1, \dots, K\):
      • Step 1: Train the model on \(K‑1\) folds.
      • Step 2: Evaluate the model on the held‑out fold.
  • The average error (e.g., deviance) across folds provides a robust estimate of model performance.

Training, Validation, and Test Datasets

  • Training Data:
    The portion of data used to fit the model.
    Within this set, k‑fold cross-validation is applied.

  • Validation Data:
    Temporary splits within the training set during cross-validation, used to tune hyperparameters and assess performance.

  • Test Data:
    A held-out dataset that is never used during model tuning.
    Provides an unbiased evaluation of the final model’s performance.

  • Workflow:

    1. Split: Divide the dataset into training and test sets.
    2. Cross-Validate: Apply k‑fold CV on the training set for model tuning and selection.
    3. Evaluate: Use the test set for final performance assessment.

Regularization

Regularization

  • Regularized regression can resolve the following problems:

    • Quasi-separation in logistic regression
    • Multicolinearity in linear regression
      • e.g., Variables \(\texttt{age}\) and \(\texttt{years_of_workforce}\) in linear regression of \(\texttt{income}\).
    • Overfitting

  • The above situations usually happen when the model is too complex (e.g., has large or many beta variables).

  • We will discuss three regularized regression methods:

    • Lasso or LASSO (least absolute shrinkage and selection operator) (L1)
    • Ridge (L2)
    • Elastic net

What is Linear Regression Doing?

  • Regular linear regression tries to find the beta parameters \(\beta_0, \beta_1, \beta_2, \,\cdots\, \beta_{p}\) such that

\[ f(x_i) = b_0 + b_1 x_{1,i} + b_2 x_{2,i} + \,\cdots\, + b_p x_{p,i} \] is as close as possible to \(y_i\) for all the training data by minimizing the sum of the squared error (SSE) between \(y\) and \(f(x)\) with observations \(i = 1, \cdots, N\), where the SSE is

\[ (y_1 - f(x_1))^2 + (y_2 - f(x_2))^2 + \,\cdots\, + (y_N - f(x_N))^2 \]

What is Lasso Regression Doing?

  • Lasso regression tries to find the beta parameters \(\beta_0, \beta_1, \beta_2, \,\cdots\, \beta_{p}\) and \(\alpha\) such that

\[ f(x_i) = b_0 + b_1 x_{1,i} + b_2 x_{2,i} + \,\cdots\, + b_p x_{p,i} \] is as close as possible to \(y_i\) for all the training data by minimizing the sum of the squared error (SSE) plus the sum of the absolute value of the beta parameters multiplied by the alpha parameter:

\[ \begin{align} &(y_1 - f(x_1))^2 + (y_2 - f(x_2))^2 + \,\cdots\, + (y_N - f(x_N))^2 \\ &+ \alpha \times(| \beta_1 | + |\beta_2 | + \,\cdots\, + |\beta_{p}|) \end{align} \] - When \(\alpha = 0\), this reduces to regular linear regression.

What is Lasso Regression Doing?

  • When variables are nearly collinear, lasso regression tends to drive one or more of them to zero.

  • In the regression of \(\text{income}\), lasso regression might give zero credit to one of the two variables, \(\texttt{age}\) and \(\texttt{years_of_workforce}\).

  • For this reason, lasso regression is often used as a form of model/variable selection.

What is Ridge Regression Doing?

  • Ridge regression tries to find the beta parameters \(\beta_0, \beta_1, \beta_2, \,\cdots\, \beta_{p}\) and \(\alpha\) such that

\[ f(x_i) = b_0 + b_1 x_{1,i} + b_2 x_{2,i} + \,\cdots\, + b_p x_{p,i} \] is as close as possible to \(y_i\) for all the training data by minimizing the sum of the squared error (SSE) plus the sum of the squared beta parameters multiplied by the alpha parameter:

\[ \begin{align} &(y_1 - f(x_1))^2 + (y_2 - f(x_2))^2 + \,\cdots\, + (y_N - f(x_N))^2 \\ &+ \alpha \times (\beta_1^2 + \beta_2^2 + \,\cdots\, + \beta_{p}^2) \end{align} \] - When \(\alpha = 0\), this reduces to regular linear regression.

What is Ridge Regression Doing?

  • When variables are nearly collinear, ridge regression tends to average the collinear variables together.
  • You can think of this as “ridge regression shares the credit.”
    • Imagine that being one year older/one year longer in the workforce increases \(\texttt{income}\) in the training data.
    • In this situation, ridge regression might give a half credit to each variable of \(\texttt{age}\) and \(\texttt{years_of_workforce}\), which adds up to the appropriate effect.

What is Elastic Net Regression Doing?

  • Elastic net regression tries to find the beta parameters \(\beta_0, \beta_1, \beta_2, \,\cdots\, \beta_{p}\) and \(\lambda\) (L1 parameter) such that

\[ f(x_i) = b_0 + b_1 x_{1,i} + b_2 x_{2,i} + \,\cdots\, + b_p x_{p,i} \] is as close as possible to \(y_i\) for all the training data by minimizing the sum of the squared error (SSE) plus a linear combination of the ridge and the lasso penalties with the \(\lambda\) parameter:

\[ \begin{align} &(y_1 - f(x_1))^2 + (y_2 - f(x_2))^2 + \,\cdots\, + (y_N - f(x_N))^2 \\ &+ \lambda \times(| \beta_1 | + |\beta_2 | + \,\cdots\, + |\beta_{p}|)\\ &+ (1-\lambda) \times(\beta_1^2 + \beta_2^2 + \,\cdots\, + \beta_{p}^2) \end{align} \]

where \(0 \leq \lambda \leq 1\).

Choosing Between Lasso, Ridge, and Elastic Net

  • In some situations, such as when you have a very large number of variables, many of which are correlated to each other, the lasso may be preferred.
  • In other situations, like quasi-separability, the ridge solution may be preferred.
  • When you are not sure which is the best approach, you can combine the two by using elastic net regression.
    • Different values of \(\lambda\) between 0 and 1 give different trade-offs between sharing the credit among correlated variables, and only keeping a subset of them.

Intuition on Different Penalties

  • Lasso (L1) Penalty (\(|\beta|\)):
    • Each unit increase in \(\beta\) adds a constant penalty, regardless of \(\beta\) ’s size.
    • Drives some coefficients exactly to zero, acting as a predictor selection mechanism.
  • Ridge (L2) Penalty (\(\beta^2\)):
    • Gently penalizes small-to-moderate deviations from zero, but penalty increases quickly for large \(\beta\).
    • Shrinks coefficients but does not set them exactly to zero.

Intuition on Different Penalties

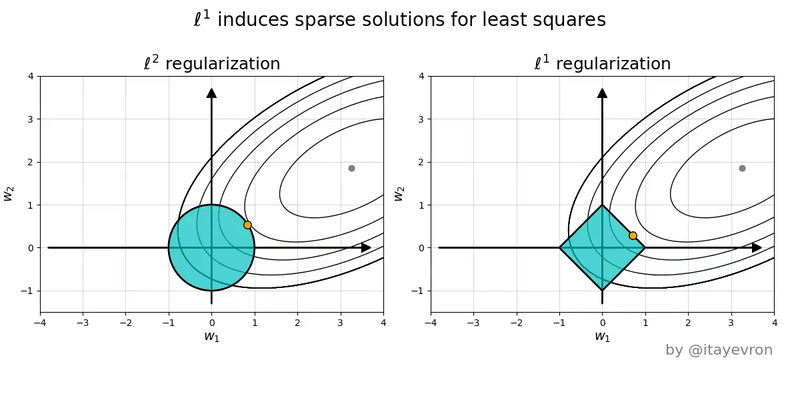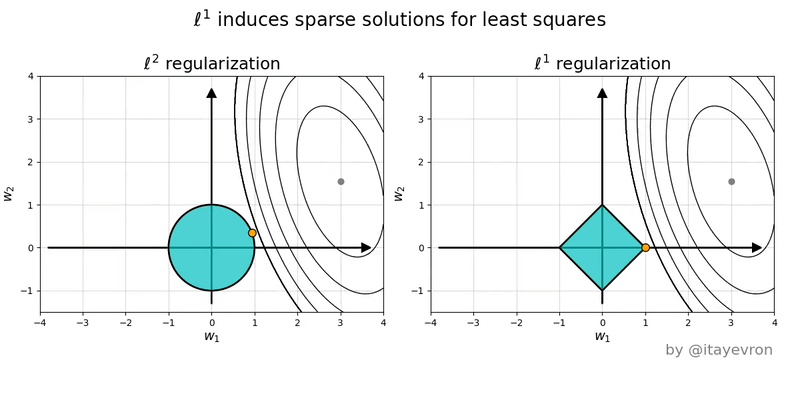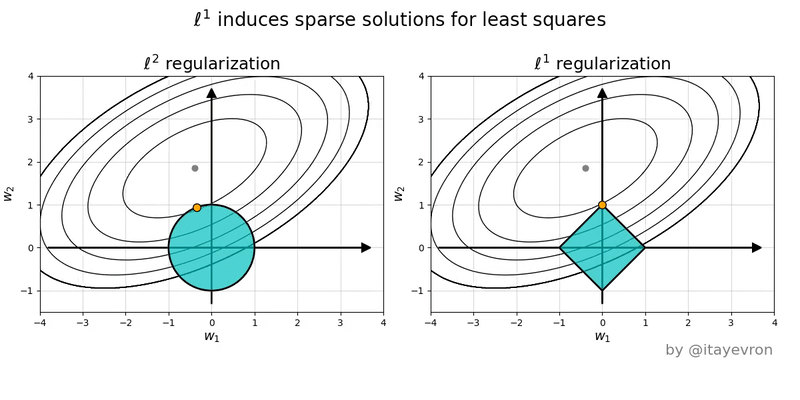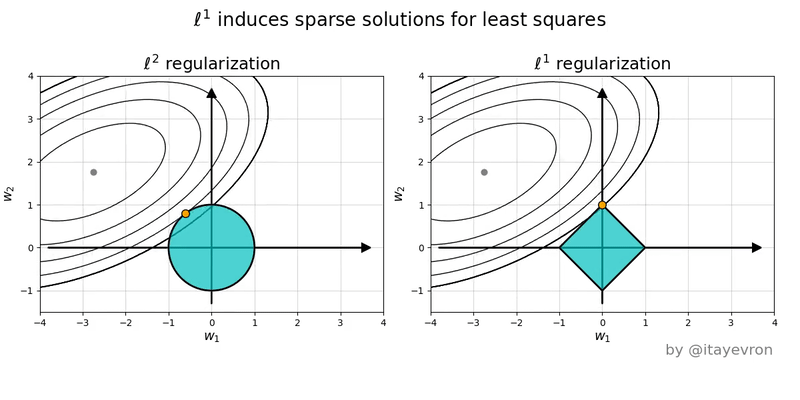
  • Lasso induces corner solutions!

Regularization Affects the Interpretation of Beta

  • No Need to Omit a Reference Category:
    • In standard regression, one dummy is typically omitted to avoid perfect multicollinearity.
      • Even though including all dummies creates perfect collinearity with an intercept, regularization resolves this by penalizing the beta parameters.
    • In regularized regression, the penalty term handles multicollinearity by shrinking all coefficients, so you can include all dummy variables.
    • Each coefficient then represents the deviation from a shared baseline (an implicit average effect).
  • Interpretation:
    • With this approach, we interpret a dummy’s beta as how much that category’s association with the outcome, without worrying about the reference level (intercept).

Regularized Regression with Cross-Validation with scikit-learn

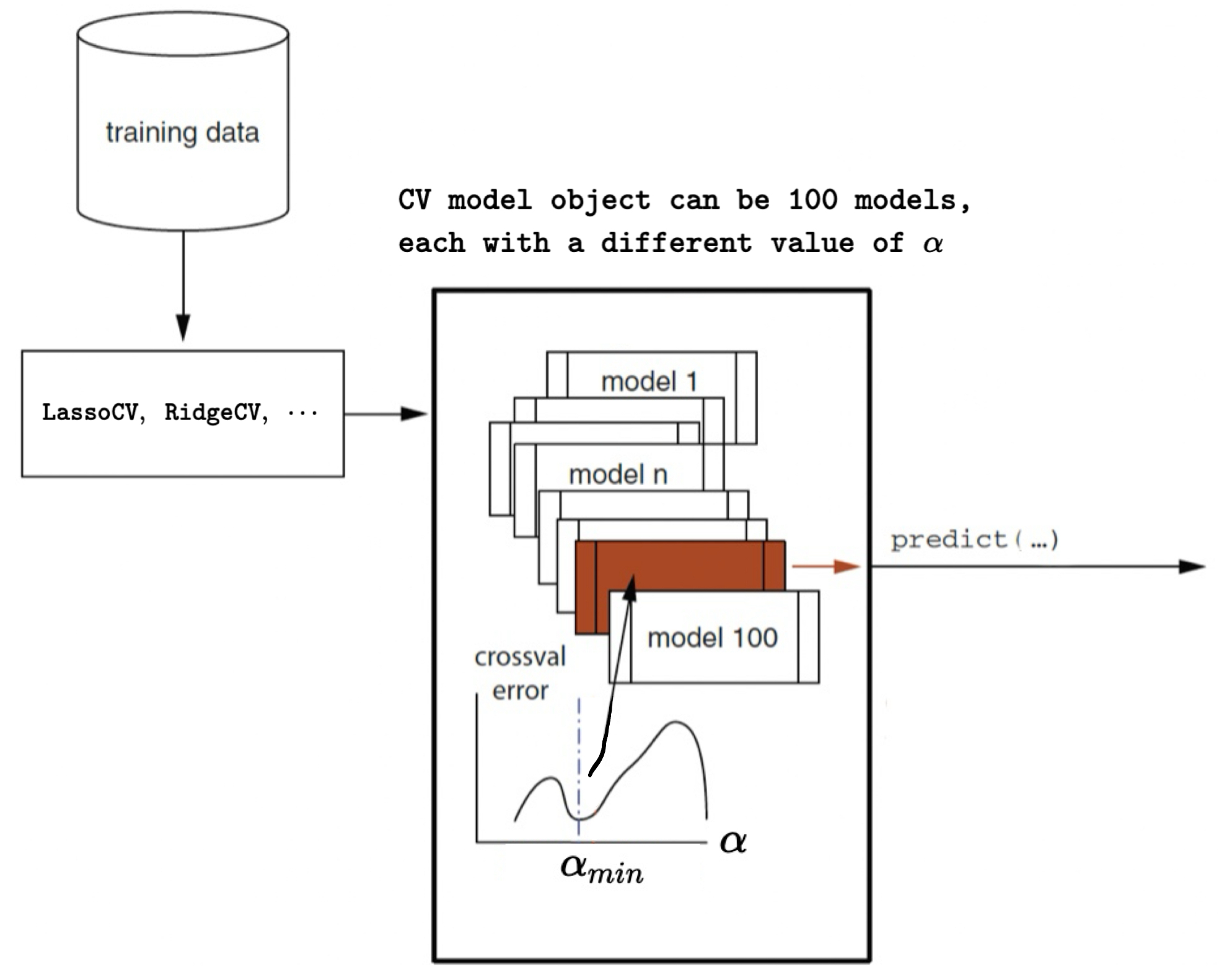
  • \(\alpha_{min}\): the \(\alpha\) for the model with the minimum cross-validation (CV) error

Regularized Logistic Regression with scikit-learn

Python Libraries and Modules for Regularization

Here are the required libraries and modules for logistic regression with regularization:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.metrics import (confusion_matrix, accuracy_score, precision_score,
                             recall_score, roc_curve, roc_auc_score)

Data Preparation with train_test_split() and pd.get_dummies()

cars = pd.read_csv('https://bcdanl.github.io/data/car-data.csv')

# Split into train and test (70% train, 30% test)
# Using a fixed random state for reproducibility (seed = 24351)
cars_train, cars_test = train_test_split(cars, test_size=0.3, random_state=24351)

# Define predictors: all columns except "rating" and "fail"
predictors = [col for col in cars.columns if col not in ['rating', 'fail']]

# One-hot encode categorical predictors.
X_train = pd.get_dummies(cars_train[predictors])
X_test = pd.get_dummies(cars_test[predictors])
# Ensure that the test set has the same dummy columns as the training set
X_test = X_test.reindex(columns=X_train.columns)

# Outcome variable
y_train = cars_train['fail'].astype(int)
y_test = cars_test['fail'].astype(int)

Lasso - LogisticRegressionCV(penalty='l1', solver='saga')

lasso_cv = LogisticRegressionCV(Cs=100, cv=5, 
  penalty='l1', solver='saga', max_iter=1000, scoring='neg_log_loss')
lasso_cv.fit(X_train, y_train)
  • Cs=100: Tries 100 different values of regularization strength (1/C)
  • cv=5: Uses 5-fold cross-validation
  • penalty='l1': Applies L1 regularization (Lasso)
  • solver='saga' Supports L1 regularization
  • max_iter=1000: Sets the maximum number of iterations for solver to converge
  • scoring='neg_log_loss': Uses deviance as the CV performance metric
  • .fit(X_train, y_train): Fits the model; Selects the best \(\alpha = \frac{1}{C}\).

Lasso Logistic Regression (L1) - Full Code

# Note: solver='saga' supports L1 regularization.
lasso_cv = LogisticRegressionCV(
    Cs=100, cv=5, penalty='l1', solver='saga', max_iter=1000, scoring='neg_log_loss'
)
lasso_cv.fit(X_train, y_train)

intercept = float(lasso_cv.intercept_)
coef_lasso = pd.DataFrame({
    'predictor': list(X_train.columns),
    'coefficient': list(lasso_cv.coef_[0])
})

print("Lasso Regression Coefficients:")
print(coef_lasso)

# Force an order for the y-axis (using the feature names as they appear in coef_lasso)
order = coef_lasso['predictor'].tolist()

plt.figure(figsize=(8,6))
ax = sns.pointplot(x="coefficient", y="predictor", data=coef_lasso, order=order, join=False)
plt.title("Coefficients of Lasso Logistic Regression Model")
plt.xlabel("Coefficient value")
plt.ylabel("Predictor")

# Draw horizontal lines from 0 to each coefficient.
for _, row in coef_lasso.iterrows():
    # Get the y-axis position from the order list.
    y_pos = order.index(row['predictor'])
    plt.hlines(y=y_pos, xmin=0, xmax=row['coefficient'], color='gray', linestyle='--')

# Draw a vertical line at 0.
plt.axvline(0, color='black', linestyle='--')

plt.show()

# Prediction and evaluation for lasso model
y_pred_prob_lasso = lasso_cv.predict_proba(X_test)[:, 1]
y_pred_lasso = (y_pred_prob_lasso > 0.5).astype(int)
ctab_lasso = confusion_matrix(y_test, y_pred_lasso)
accuracy_lasso = accuracy_score(y_test, y_pred_lasso)
precision_lasso = precision_score(y_test, y_pred_lasso)
recall_lasso = recall_score(y_test, y_pred_lasso)
auc_lasso = roc_auc_score(y_test, y_pred_prob_lasso)

print("Confusion Matrix (Lasso):\n", ctab_lasso)
print("Lasso Accuracy:", accuracy_lasso)
print("Lasso Precision:", precision_lasso)
print("Lasso Recall:", recall_lasso)


# Plot ROC Curve
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob_lasso)
plt.figure(figsize=(8,6))
plt.plot(fpr, tpr, label=f'Lasso (AUC = {auc_ridge:.2f})')
plt.plot([0, 1], [0, 1], 'k--', label='Random Guess')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve for Lasso Logistic Regression Model')
plt.legend(loc='best')
plt.show()

Ridge (L2) - LogisticRegressionCV(penalty='l2')

ridge_cv = LogisticRegressionCV(Cs=100, cv=5, 
  penalty='l2', solver='lbfgs', max_iter=1000, scoring='neg_log_loss'
)
ridge_cv.fit(X_train, y_train)
  • penalty='l2': Applies L2 regularization (Ridge)
  • solver='lbfgs' Supports L2 regularization (optional)

Ridge Logistic Regression (L2) - Full Code

# LogisticRegressionCV automatically selects the best regularization strength.
ridge_cv = LogisticRegressionCV(
    Cs=100, cv=5, penalty='l2', solver='lbfgs', max_iter=1000, scoring='neg_log_loss'
)
ridge_cv.fit(X_train, y_train)

print("Ridge Regression - Best C (inverse of regularization strength):", ridge_cv.C_[0])
intercept = float(ridge_cv.intercept_)
coef_ridge = pd.DataFrame({
    'predictor': list(X_train.columns),
    'coefficient': list(ridge_cv.coef_[0])
})
print("Ridge Regression Coefficients:")
print(coef_ridge)

# Force an order for the y-axis (using the feature names as they appear in coef_ridge)
order = coef_ridge['predictor'].tolist()

plt.figure(figsize=(8,6))
ax = sns.pointplot(x="coefficient", y="predictor", data=coef_ridge, order=order, join=False)
plt.title("Coefficients of Ridge Logistic Regression Model")
plt.xlabel("Coefficient value")
plt.ylabel("Predictor")

# Draw horizontal lines from 0 to each coefficient.
for _, row in coef_ridge.iterrows():
    # Get the y-axis position from the order list.
    y_pos = order.index(row['predictor'])
    plt.hlines(y=y_pos, xmin=0, xmax=row['coefficient'], color='gray', linestyle='--')

# Draw a vertical line at 0.
plt.axvline(0, color='black', linestyle='--')
plt.show()

# Prediction and evaluation for ridge model
y_pred_prob_ridge = ridge_cv.predict_proba(X_test)[:, 1]
y_pred_ridge = (y_pred_prob_ridge > 0.5).astype(int)
ctab_ridge = confusion_matrix(y_test, y_pred_ridge)
accuracy_ridge = accuracy_score(y_test, y_pred_ridge)
precision_ridge = precision_score(y_test, y_pred_ridge)
recall_ridge = recall_score(y_test, y_pred_ridge)
auc_ridge = roc_auc_score(y_test, y_pred_prob_ridge)

print("Confusion Matrix (Ridge):\n", ctab_ridge)
print("Ridge Accuracy:", accuracy_ridge)
print("Ridge Precision:", precision_ridge)
print("Ridge Recall:", recall_ridge)


# Plot ROC Curve
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob_ridge)
plt.figure(figsize=(8,6))
plt.plot(fpr, tpr, label=f'Ridge (AUC = {auc_ridge:.2f})')
plt.plot([0, 1], [0, 1], 'k--', label='Random Guess')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve for Ridge Logistic Regression Model')
plt.legend(loc='best')
plt.show()

Elastic Net - LogisticRegressionCV(penalty='l2')

enet_cv = LogisticRegressionCV(
    Cs=10, cv=5, penalty='elasticnet', solver='saga',
    l1_ratios=[0.5, 0.7, 0.9], max_iter=1000, scoring='neg_log_loss'
)
enet_cv.fit(X_train, y_train)
  • Cs=10: Tries 10 different values of regularization strength (1/C)
  • cv=5: Uses 5-fold cross-validation
  • penalty='elasticnet': Applies Elastic Net regularization
  • l1_ratios = [0.5, 0.7, 0.9] In this model, we try 0.5, 0.7, 0.9
    • l1_ratio = 1 → Lasso
      • l1_ratio = 0 → Ridge

Elastic Net Logistic Regression - Full Code

# LogisticRegressionCV supports elastic net penalty with solver 'saga'.
# l1_ratio specifies the mix between L1 and L2 (0 = ridge, 1 = lasso).
enet_cv = LogisticRegressionCV(
    Cs=10, cv=5, penalty='elasticnet', solver='saga',
    l1_ratios=[0.5, 0.7, 0.9], max_iter=1000, scoring='neg_log_loss'
)
enet_cv.fit(X_train, y_train)

print("Elastic Net Regression - Best C:", enet_cv.C_[0])
print("Elastic Net Regression - Best l1 ratio:", enet_cv.l1_ratio_[0])

intercept = float(enet_cv.intercept_)
coef_enet = pd.DataFrame({
    'predictor': list(X_train.columns),
    'coefficient': list(enet_cv.coef_[0])
})
print("Elastic Net Regression Coefficients:")
print(coef_enet)


# Force an order for the y-axis (using the feature names as they appear in coef_lasso)
order = coef_enet['predictor'].tolist()

plt.figure(figsize=(8,6))
ax = sns.pointplot(x="coefficient", y="predictor", data=coef_enet, order=order, join=False)
plt.title("Coefficients of Elastic Net Logistic Regression Model")
plt.xlabel("Coefficient value")
plt.ylabel("Predictor")

# Draw horizontal lines from 0 to each coefficient.
for _, row in coef_enet.iterrows():
    # Get the y-axis position from the order list.
    y_pos = order.index(row['predictor'])
    plt.hlines(y=y_pos, xmin=0, xmax=row['coefficient'], color='gray', linestyle='--')

# Draw a vertical line at 0.
plt.axvline(0, color='black', linestyle='--')

plt.show()

# Prediction and evaluation for elastic net model
y_pred_prob_enet = enet_cv.predict_proba(X_test)[:, 1]
y_pred_enet = (y_pred_prob_enet > 0.5).astype(int)
ctab_enet = confusion_matrix(y_test, y_pred_enet)
accuracy_enet = accuracy_score(y_test, y_pred_enet)
precision_enet = precision_score(y_test, y_pred_enet)
recall_enet = recall_score(y_test, y_pred_enet)

print("Confusion Matrix (Elastic Net):\n", ctab_enet)
print("Elastic Net Accuracy:", accuracy_enet)
print("Elastic Net Precision:", precision_enet)
print("Elastic Net Recall:", recall_enet)

Regularized Linear Regression with scikit-learn

Lasso Linear Regression

  • The browser dataset contains web browsing logs for 10,000 households.
  • The browser dataset include a year’s worth of their browser logs for the 1,000 most heavily trafficked websites
  • Each browser in the sample spent at least $1 online in the same year.

\[ \log(\text{spend}_{i}) = \beta_0 + \beta_1 X_{1,i} +\,\cdots\,+ \beta_{1000} X_{1000,i} + \epsilon_i \] - \(\text{spend}_{i}\): household \(i\)’s amount of dollars spent on online shopping - \(X_{p, i}\) household \(i\)’s percentage of visiting the \(p\) website

Lasso Linear Regression - Libraries and Modules

from google.colab import data_table
data_table.enable_dataframe_formatter()  # Enabling an interactive DataFrame display
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.preprocessing import scale   # zero mean & one s.d.
from sklearn.linear_model import LassoCV, lasso_path
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

Lasso Linear Regression - Data Prep

df = pd.read_csv("https://bcdanl.github.io/data/browser-online-shopping.zip")

X = df.drop('spend', axis = 1)
y = df['spend']

# Train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

X_train_np = X_train.values
X_test_np = X_test.values
y_train_np = y_train.values
y_test_np = y_test.values

Lasso Linear Regression - Fitting the Model

# LassoCV with a range of alpha values
lasso_cv = LassoCV(n_alphas = 100, # default is 100
                   alphas = None, # alphas=None automatically generate 100 candidate alpha values
                   cv = 5, 
                   random_state=42,
                   max_iter=100000)
lasso_cv.fit(X_train, np.log(y_train))

Lasso Linear Regression - Results

# Best alpha
print("LassoCV - Best alpha:", lasso_cv.alpha_)

# Create a DataFrame including the intercept and the coefficients:
coef_lasso = pd.DataFrame({
    'predictor': list(X_train.columns),
    'coefficient':  list(lasso_cv.coef_),
    'exp_coefficient': np.exp(  list(lasso_cv.coef_) )
})

# Evaluate
y_pred_lasso = lasso_cv.predict(X_test)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
print("LassoCV - MSE:", mse_lasso)

coef_lasso = coef_lasso.query('coefficient != 0')
coef_lasso.shape[0]
coef_lasso.sort_values('coefficient', ascending = False)

Lasso Path - CV Errors as as a Function of Alpha

# Compute the mean and standard deviation of the CV errors for each alpha.
mean_cv_errors = np.mean(lasso_cv.mse_path_, axis=1)
std_cv_errors = np.std(lasso_cv.mse_path_, axis=1)

plt.figure(figsize=(8, 6))
plt.errorbar(lasso_cv.alphas_, mean_cv_errors, yerr=std_cv_errors, marker='o', linestyle='-', capsize=5)
plt.xscale('log')
plt.xlabel('Alpha')
plt.ylabel('Mean CV Error (MSE)')
plt.title('Cross-Validation Error vs. Alpha')
plt.axvline(x=lasso_cv.alpha_, color='red', linestyle='--', label='Best alpha')
plt.legend()
plt.show()

Lasso Path - Beta Estimates as a Function of Alpha

# Compute the lasso path. Note: we use np.log(y_train) because that's what you used in LassoCV.
alphas, coefs, _ = lasso_path(X_train, np.log(y_train), alphas=lasso_cv.alphas_, max_iter=100000)

plt.figure(figsize=(8, 6))
# Iterate over each predictor and plot its coefficient path.
for i, col in enumerate(X_train.columns):
    plt.plot(alphas, coefs[i, :], label=col)

plt.xscale('log')
plt.xlabel('Alpha')
plt.ylabel('Coefficient value')
plt.title('Lasso Coefficient Paths')
plt.axvline(x=lasso_cv.alpha_, color='red', linestyle='--', label='Best alpha')
plt.show()

Lasso Path - The Number of Nonzero Betas as a Function of Alpha

# Compute the coefficient path over the alpha grid that LassoCV used
alphas, coefs, _ = lasso_path(X_train, np.log(y_train),
                              alphas=lasso_cv.alphas_,
                              max_iter=100000)

# Count nonzero coefficients for each alpha (coefs shape: (n_features, n_alphas))
nonzero_counts = np.sum(coefs != 0, axis=0)

# Plot the number of nonzero coefficients versus alpha
plt.figure(figsize=(8,6))
plt.plot(alphas, nonzero_counts, marker='o', linestyle='-')
plt.xscale('log')
plt.xlabel('Alpha')
plt.ylabel('Number of nonzero coefficients')
plt.title('Nonzero Coefficients vs. Alpha')
#plt.gca().invert_xaxis()  # Lower alphas (less regularization) on the right
plt.axvline(x=lasso_cv.alpha_, color='red', linestyle='--', label='Best alpha')
plt.legend()
plt.show()

Hockey Player Performance via Regularized Logistic Regression

Background and Motivation

  • The player “plus-minus” (PM) is a common hockey performance metric.
  • The classic PM is a function of goals scored while that player is on the ice:
    • the number of goals for his team minus the number against.
  • The limits of this approach are obvious: there is no accounting for teammates or opponents.
  • In hockey, where players tend to be grouped together on “lines” and coaches will “line match” against opponents, a player’s PM can be artificially inflated or deflated by the play of his opponents and peers.

Data

  • The data comprise of play-by-play NHL game data for regular and playoff games during 11 seasons of 2002-2003 through 2013-2014.

  • There were p = 2,439 players involved in n = 69,449 goals.

  • The data contains information that indicates seasons, home & away teams, team configuration such as 5 on 4 powerplay, and which players are on & off the ice when a goal is made, etc.

  • Unfortunately, Python scikit-learn is not optimized to handle all season’s data.

    • What we can do with Python scikit-learn is handling one season each.
    • I highly recommend R’s glmnet for regression with cross-validation.

Data

nhl = pd.read_csv('https://bcdanl.github.io/data/NHL_data_2002_2003.csv')
  • homegoal: an indicator (0 or 1) for the home team scoring
  • player_name: entries for who was on the ice for each goal
  • team: indicators for each team
  • config: Special teams info. E.g., S5v4 is a 5 on 4 powerplay
  • The value of config, team, and player_name are:
    • 1 if it is for the home-team
    • -1 for the away team
    • 0 otherwise

Model

  • Consider constructing a binary response for every goal, equal to 1 for home-team goals and 0 for away-team goals:

\[ \begin{align} \log\left(\frac{\text{Prob}(\text{home-goal}_{i})}{\text{Prob}(\text{away-goal}_{i})}\right) &= \beta_0 + \sum_{j=1}^{J} \beta_{\text{team}_{j}}\text{team}_{j, i} + \sum_{k=1}^{K} \beta_{\text{config}_{k}}\text{config}_{k, i} \\ &\qquad + \sum_{m=1}^{M} \beta_{\text{home-player}_{m}}\text{home-player}_{m, i}\\ &\qquad - \sum_{n=1}^{N} \beta_{\text{away-player}_{n}}\text{away-player}_{n, i} \end{align} \]

Home-ice Advantage

  • How can we estimate the home-team effect?
np.exp(lasso_cv.intercept_)
  • This is the effect on odds that a goal is home rather than away, regardless of any information about what teams are playing or who is on ice.

Player’s Impact

  • How can we estimate the player effect?
np.exp(lasso_cv.coef_[0])
  • Whenever a goal is scored in the season 2002-2003, …
    • Colorado’s odds of having scored (rather than having been scored on) increase by 160% if Peter Forsberg is on the ice.

Traditional Plus‑Minus vs. Expected Plus‑Minus

  • Traditional Plus‑Minus (PM)
    • Definition: Sum of on-ice contributions; +1 for a goal scored for the player’s team and -1 for a goal against.
    • Limitations: Can be noisy due to team context, limited ice time, or random variation.
  • Expected Plus‑Minus (ppm)
    • Definition: A model-based estimate of a player’s impact.
    • Calculation:
      • Convert a player’s effect (\(\beta\)) to a probability: \(p = \frac{e^{\beta}}{1 + e^{\beta}}\)
      • Compute expected PM as: \(\text{ppm} = ng \times p − ng \times (1−p )\)
      • \(ng\): the total number of goals the player was on the ice.
    • Benefits: Smooths out noise and adjusts for context.

Traditional Plus‑Minus vs. Expected Plus‑Minus

  • Observed vs. Modeled:
    • PM is a raw, observed measure.
    • Expected PM leverages model estimates to predict performance.
  • Variability:
    • PM may fluctuate due to external factors.
    • Expected PM attempts to isolate a player’s true impact.
  • Applications:
    • Expected PM can help identify under- or over-performing players and guide strategic decisions.

Scaling?

  • We do not want to standardize variables here.
    • The penalty with standardization is \(\alpha \times SD(X_{player})\)
    • Players with small SD are those who play little (almost all zeros).
    • Players with large SD are those who play a lot.
    • Standardization would up-weight the influence of players who rarely play relative to those who have a lot of ice time.
  • Re-do everything with
from sklearn.preprocessing import scale # zero mean & one s.d.
Xpred = scale(nhl_train)

Omitted Variable Bias

Omitted Variable Bias

  • Omitted variable bias (OVB): bias in the model because of omitting an important predictor that is correlated with existing predictor(s).

  • Let’s use an orange juice (OJ) example to demonstrate the OVB.

    • OJ price elasticity estimates vary with models, whether or not taking into account brand or ad_status

Short- and Long- Regressions

  • OVB is the difference in beta estimates between short- and long-form regressions.

  • Short regression: The regression model with less predictors

\[ \begin{align} \log(\text{sales}_i) = \beta_0 + \beta_1\log(\text{price}_i) + \epsilon_i \end{align} \]

  • Long regression: The regression model that adds additional predictor(s) to the short one.

\[ \begin{align} \log(\text{sales}_i) =& \beta_0 + \beta_{1}\log(\text{price}_i) \\ &+ \beta_{2}\text{minute.maid}_i + \beta_{3}\text{tropicana}_i + \epsilon_i \end{align} \] - OVB for \(\beta_1\) is:

\[ \text{OVB} = \widehat{\beta_{1}^{short}} - \widehat{\beta_{1}^{long}} \]

OVB formula

  • Consider the following short- and long- regressions:

    • Short: \(Y_i = \beta_0 + \beta_{1}^{short}X_1 + \epsilon_{short}\)
    • Long: \(Y_i = \beta_0 + \beta_{1}^{long}X_1 +\beta_{2}X_2 + \epsilon_{long}\)

  • Error in short form can be represented as: \[ {\epsilon_{short}} = \beta_{2}X_2 + \epsilon_{long} \]

  • If variable \(X_1\) is correlated with \(X_2\), the following assumptions are violated in the short regression model:

    • Errors are not correlated with predictors.
    • Errors have a mean value of 0.

How does an OVB happen in regression?

  • In the first stage, consider the relationship between price and brand:

\[ \log(\text{price}) = \beta_0 + \beta_1\text{minute_maid} + \beta_2\text{tropicana} + \epsilon_{1st} \]

  • Then, calculate the residual: \[ \widehat{\epsilon_{1st}} = \log(\text{price}) - \widehat{\log(\text{price})} \]

  • The residual represents the log of OJ price after its correlation with brand has been removed!

  • In the second stage, regress \(\log(\text{sales})\) on residual \(\widehat{\epsilon_{1st}}\):

\[ \log(\text{sales}) = \beta_0 + \beta_1\widehat{\epsilon_{1st}} + \epsilon_{2nd} \]

Regression Sensitivity Analysis

  • Regression finds the coefficients on the part of each predictor that is independent from the other predictors.

  • What can we do to deal with OVB problems?

    • Because we can never be sure whether a given set of controls is enough to eliminate OVB, it’s important to ask how sensitive regression results are to changes in the list of controls.