Lecture 8

Logistic Regression

Byeong-Hak Choe

bchoe@geneseo.edu

SUNY Geneseo

March 10, 2025

Logistic Regression

Motivation

• Relationship: Suppose we want to know how much the flight’s origin/destination, weather, and air carrier is associated with the probability that a flight will be delayed.
• Prediction: Suppose we also want to predict whether or not a flight will be delayed, based on facts like the flight’s origin/destination, weather, and air carrier.
• For every flight \(\texttt{i}\), you want to predict \(\texttt{flight_delayed[i]}\), a binary variable ( \(\texttt{TRUE}\) or \(\texttt{FALSE}\)), based on \(\texttt{origin[i]}\), \(\texttt{destination[i]}\), \(\texttt{weather[i]}\), and \(\texttt{air_carrier[i]}\).
  • Prediction of a binary variable \(y_{i}\) (0 or 1) is the expected value of \(y_{i}\)—the predicted probability that \(y_{i} = 1\).

Motivation

• The logistic regression model for the probability that a flight will be delayed is formulated as: \[ \begin{align} &\quad\texttt{ Prob( flight_delayed[i] == TRUE ) } \\[.5em] &=\, \texttt{G( b$_{\texttt{0}}$ + b$_{\texttt{origin}}$*origin[i] }\\ &\qquad\quad\,\, + \texttt{b$_{\texttt{destination}}$*destination[i] }\\ &\qquad\quad\,\, + \texttt{b$_{\texttt{weather}}$*weather[i] }\\ &\qquad\quad\,\, + \texttt{b$_{\texttt{air_carrier}}$*air_carrier[i] )}. \end{align} \]

• \(G(z_i)\): the logistic function

\[ \begin{align} \texttt{G(z[i]) = } \dfrac{\texttt{exp(z[i])}}{\texttt{1 + exp(z[i])}}.\notag \end{align} \]

Properties of the Logistic Function

• The logistic function \(G(z_i)\) maps the linear combination of predictors to the probability that the outcome \(y_{i}\) is \(1\).

• \(z_{i} = b_{0} + b_{1}x_{1, i} + b_{2}x_{2, i} + \,\cdots\, + x_{k, i}\)

• \(z_{i} \overset{G}{\rightarrow} \texttt{ Prob} ( y_{i} = 1 )\)

Properties of the Logistic Function

• The logistic function \(G(z_i)\) \[ \begin{align} G(z_i) = \frac{\exp(z_i)}{1 + \exp(z_i)} \end{align} \] ranges between 0 and 1 for any value of \(z_i\)

What is the Logistic Regression doing?

• The logistic regression finds the beta coefficients, \(b_0\), \(b_1\), \(b_2\), \(\cdots\), \(b_{k}\) such that the logistic function \[ G(b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i}) \] is the best possible estimate of the binary outcome \(y_{i}\).

What is the Logistic Regression doing?

• The function \(G(z_i)\) is called the logistic function because the function \(G(z_i)\) is the inverse function of a logit (or a log-odd) of the probability that the outcome \(y_{i}\) is 1. \[ \begin{align} G^{-1}(z_i) &\,\equiv\, \text{logit} (\text{Prob}(y_{i} = 1))\\ &\,\equiv \log\left(\, \frac{\text{Prob}(y_{i} = 1)}{\text{Prob}(y_{i} = 0)} \,\right)\\ &\,=\, b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i} \end{align} \]

• Logistic regression is a linear regression model for log odds.

What is the Logistic Regression doing?

• Logistic regression can be expressed as linear regression of log odds of \(y_{i} = 1\) on predictors \(x_1, x_2, \cdots, x_k\):

\[ \begin{align} \text{Prob}(y_{i} = 1) &\,=\, G( b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i} )\\ \text{ }\\ \Leftrightarrow\qquad \log\left(\dfrac{\text{Prob}( y_i = 1 )}{\text{Prob}( y_i = 0 )}\right) &\,=\, b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i} \end{align} \]

Assessing Newborn Babies at Risk

• Newborn babies are assessed at one and five minutes after birth using what’s called the Apgar test, which is designed to determine if a baby needs immediate emergency care or extra medical attention.
  • A baby who scores below 7 (on a scale from 0 to 10) on the Apgar scale needs extra attention.
• Such at-risk babies are rare, so the hospital doesn’t want to provision extra emergency equipment for every delivery.
  
• On the other hand, at-risk babies may need attention quickly, so provisioning resources proactively to appropriate deliveries can save lives.

Assessing Newborn Babies at Risk

dfpd = pd.read_csv('https://bcdanl.github.io/data/NatalRiskData.csv')

• We’ll use a sample dataset from the 2010 CDC natality public-use data file.
• The data set records information about all US births, including facts about the mother and father, and about the delivery.
• The sample has just over 26,000 births in a DataFrame.

Assessing Newborn Babies at Risk

Variable	Type	Description
atRisk	Bool	1 if Apgar < 7, 0 otherwise
PWGT	Num	Prepregnancy weight
UPREVIS	Int	Prenatal visits
CIG_REC	Bool	1 if smoker, 0 otherwise
GESTREC3	Cat	< 37 weeks or ≥ 37 weeks
DPLURAL	Cat	Single / Twin / Triplet+
ULD_MECO	Bool	1 if heavy meconium
ULD_PRECIP	Bool	1 if labor < 3 hours
ULD_BREECH	Bool	1 if breech birth
URF_DIAB	Bool	1 if diabetic
URF_CHYPER	Bool	1 if chronic hypertension
URF_PHYPER	Bool	1 if pregnancy hypertension
URF_ECLAM	Bool	1 if eclampsia

Assessing Newborn Babies at Risk

• Task 1. Identify the relationship between a predictor and the probability of \(\texttt{atRisk == TRUE}\).
• Task 2. Identify ahead of time situations with a higher probability of \(\texttt{atRisk == TRUE}\).

Building a Logistic Regression Model in PySpark

• The function to build a logistic regression model in PySpark is \(\texttt{GeneralizedLinearRegression(family="binomial", link="logit")}\).
• The outcome variable \(y\) is the binary variable \(\texttt{atRisk}\) (0 or 1).
• The other variables in the table in the previous slide are predictors \(x_{k}\).
• The arguments \(\texttt{family="binomial"}\) and \(\texttt{link="logit"}\) specify the logistic distribution of the outcome variable \(y\).

from pyspark.ml.regression import GeneralizedLinearRegression

dummy_cols_GESTREC3, ref_category_GESTREC3 = add_dummy_variables('GESTREC3', 1)
dummy_cols_DPLURAL, ref_category_DPLURAL = add_dummy_variables('DPLURAL', 0)

# assembling predictors
x_cols = ['PWGT', 'UPREVIS', 'CIG_REC', 
          'ULD_MECO', 'ULD_PRECIP', 'ULD_BREECH', 'URF_DIAB',
          'URF_CHYPER', 'URF_PHYPER', 'URF_ECLAM']

assembler_predictors = (
    x_cols +
    dummy_cols_GESTREC3 + dummy_cols_DPLURAL
)

assembler_1 = VectorAssembler(
    inputCols = assembler_predictors,
    outputCol = "predictors"
)

dtrain_1 = assembler_1.transform(dtrain)
dtest_1  = assembler_1.transform(dtest)

# training model
model_1 = (
    GeneralizedLinearRegression(featuresCol="predictors",
                                labelCol="atRisk",
                                family="binomial", 
                                link="logit")
    .fit(dtrain_1)
)

# making prediction
dtrain_1 = model_1.transform(dtrain_1)
dtest_1 = model_1.transform(dtest_1)

Deviance and Likelihood

model_1.summary

• Deviance is a measure of the distance between the data and the estimated model.

\[ \text{Deviance} = -2 \log(\text{Likelihood}) + C, \] where \(C\) is constant that we can ignore.

Deviance and Likelihood

• Logistic regression finds the beta coefficients, \(b_0, b_1, \,\cdots, b_k\) , such that the logistic function

\[ G(b_0 + b_{1}x_{1,i} + b_{2}x_{2,i} + \,\cdots\, + b_{k}x_{k,i}) \]

is the best possible estimate of the binary outcome \(y_i\).

• Logistic regression finds the beta parameters that maximize the log likelihood of the data, given the model, which is equivalent to minimizing the sum of the residual deviances.

  • When you minimize the deviance, you are fitting the parameters to make the model and data look as close as possible.

Likelihood Function

• Likelihood is the probability of your data given the model.

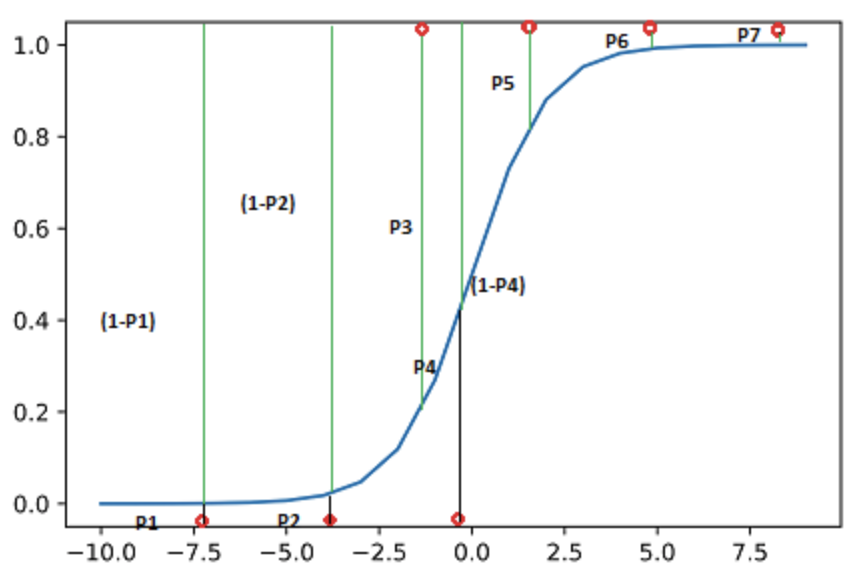
• The probability that the seven data points would be observed:
  • \(L = (1-P1)*(1-P2)* P3*(1-P4)*P5*P6*P7\)
• The log of the likelihood: \[ \begin{align} \log(L) &= \log(1-P1) + \log(1-P2) + \log(P3) \\ &\quad+ \log(1-P4) + \log(P5) + \log(P6) + \log(P7) \end{align} \]

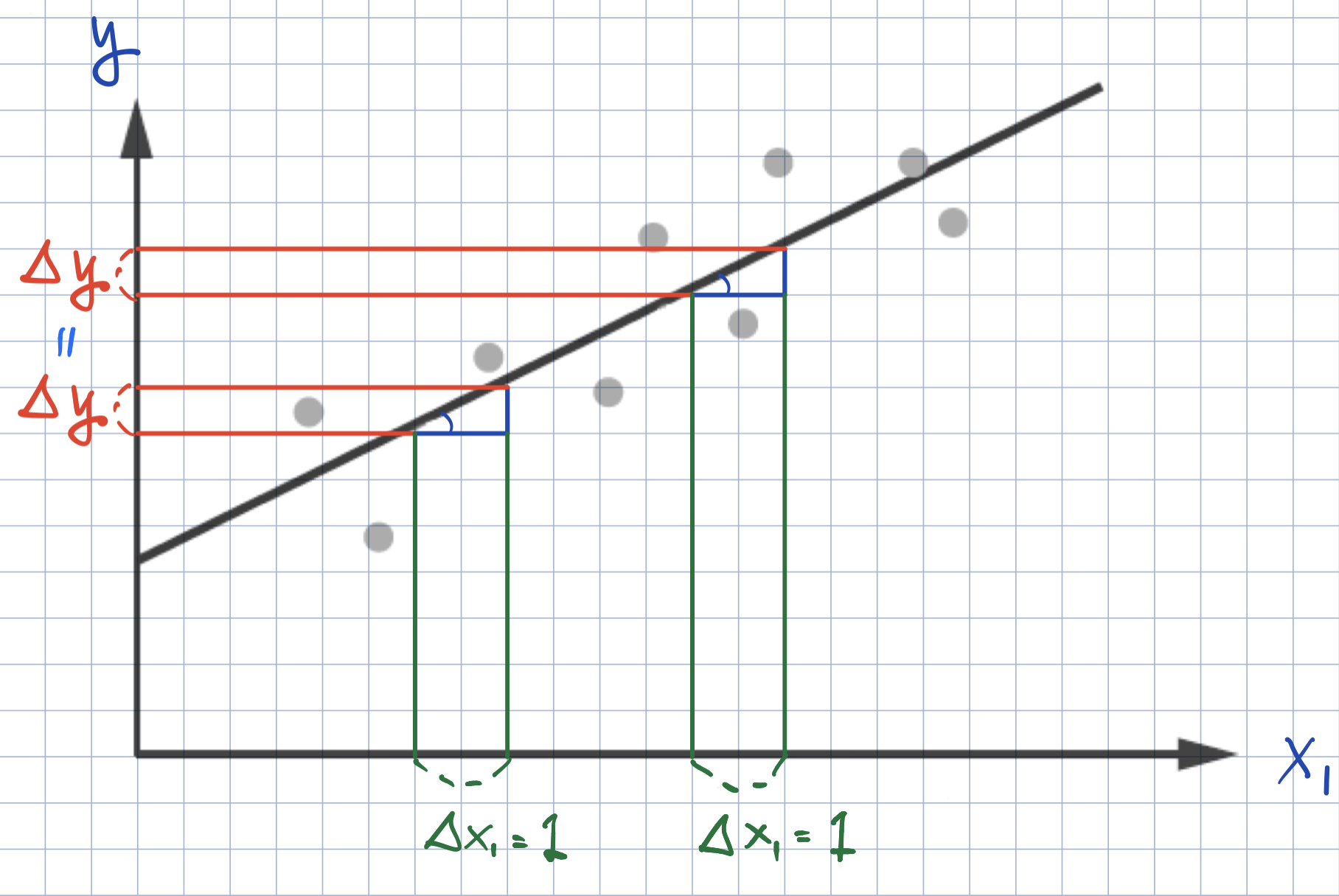
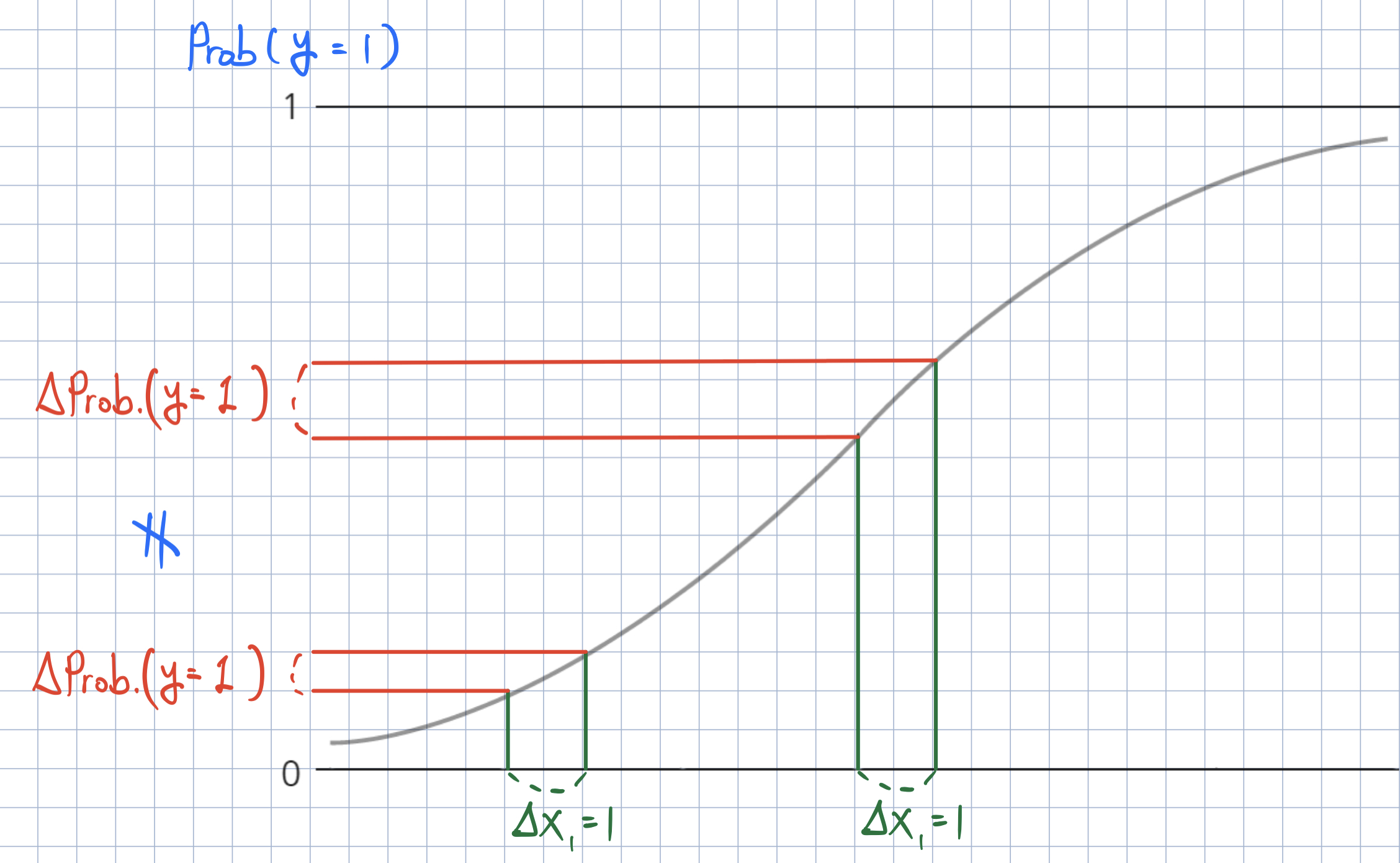
Marginal Effects

Marginal Effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\)?

model_1.summary

• If the baby is prematurely born, the log-odds of being at risk increases by 1.539 relative to the non-premature baby.

Marginal Effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\)

• In logistic regression, the effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\) is different for each observation \(i\).

Linear regression

Logistic regression

Marginal Effect of \(x_{k, i}\) on \(\text{Prob}(y_{i} = 1)\)

• How can we calculate the effect of \(x_{k, i}\) on the probability of \(y_{i} = 1\)?
  1. Marginal effect at the mean (MEM): We can obtain the marginal effect at an average observation or representative observations in the training data (MEM) or at representative values (MER)).
  2. Average marginal effect (AME): We can average the marginal effects across the training data.

def marginal_effects(model, means):
    """
    Compute marginal effects for all predictors in a PySpark GeneralizedLinearRegression model (logit)
    and return a formatted table with statistical significance.
    
    Parameters:
        model: Fitted GeneralizedLinearRegression model (with binomial family and logit link).
        means: List of mean values for the predictor variables.
    
    Returns:
        A formatted string containing the marginal effects table.
    """
    global assembler_predictors  # Use the global assembler_predictors list
    
    # Extract model coefficients, standard errors, and intercept
    coeffs = np.array(model.coefficients)
    std_errors = np.array(model.summary.coefficientStandardErrors)
    intercept = model.intercept
    
    # Compute linear combination of means and coefficients (XB)
    XB = np.dot(means, coeffs) + intercept
    
    # Compute derivative of logistic function (G'(XB))
    G_prime_XB = np.exp(XB) / ((1 + np.exp(XB)) ** 2)
    
    # Helper: significance stars.
    def significance_stars(p):
        if p < 0.01:
            return "***"
        elif p < 0.05:
            return "**"
        elif p < 0.1:
            return "*"
        else:
            return ""
    
    # Create table to store results
    results = []
    
    for i, predictor in enumerate(assembler_predictors):
        # Compute marginal effect
        marginal_effect = G_prime_XB * coeffs[i]
        
        # Compute standard error of the marginal effect
        std_error = G_prime_XB * std_errors[i]
        
        # Compute z-score and p-value
        z_score = marginal_effect / std_error if std_error != 0 else np.nan
        p_value = 2 * (1 - norm.cdf(abs(z_score))) if not np.isnan(z_score) else np.nan
        
        # Compute confidence interval (95%)
        ci_lower = marginal_effect - 1.96 * std_error
        ci_upper = marginal_effect + 1.96 * std_error
        
        # Append results
        results.append([predictor, f"{marginal_effect: .4f}", significance_stars(p_value), f"{ci_lower: .4f}", f"{ci_upper: .4f}"])
    
    # Convert results to tabulated format
    table_str = tabulate(results, headers=["Variable", "Marginal Effect", "Significance", "95% CI Lower", "95% CI Upper"], 
                         tablefmt="pretty", colalign=("left", "decimal", "left", "decimal", "decimal"))
    
    return table_str

# Example usage:
# means = [0.5, 30]  # Mean values for x1 and x2
# assembler_predictors = ['x1', 'x2']  # Define globally before calling the function
# table_output = mfx_glm(fitted_model, means)
# print(table_output)

% vs. % point

• Let’s say you have money in a savings account. The interest is 3%.
• Now consider two scenarios:
  1. The bank increases the interest rate by one percent.
  2. The bank increases the interest rate by one percentage point.
• What is the new interest rate in each scenario? Which is better?

Logistic Regression

Interpreting the Marginal Effect

• How do we interpret the ME? All else being equal,
  • There is a 2.05 percentage point increase in the probability of a newborn being at risk if the baby is prematurely born.
  • There is a 0.04 percentage point decrease in the probability of a newborn being at risk for each additional parental medical visit.

Classification

Classifier

• Your goal is to use the logistic regression model to classify newborn babies into one of two categories—at-risk or not.
• Prediction from the logistic regression with a threshold on the predicted probabilities can be used as a classifier.
  • If the predicted probability that the baby \(\texttt{i}\) is at risk is greater than the threshold, the baby \(\texttt{i}\) is classified as at-risk.
  • Otherwise, the baby \(\texttt{i}\) is classified as not-at-risk.

Double Density Plot – Choosing the Optimal Threshold

• Double density plot is useful when picking the classifier threshold.
  • Since the classifier is built using the training data, the threshold should also be selected using the training data.

import matplotlib.pyplot as plt
import seaborn as sns

# Filter training data for atRisk == 1 and atRisk == 0
pdf = dtrain_1.select("prediction", "atRisk").toPandas()

train_true = pdf[pdf["atRisk"] == 1]
train_false = pdf[pdf["atRisk"] == 0]

# Create the first density plot
plt.figure(figsize=(8, 6))
sns.kdeplot(train_true["prediction"], label="TRUE", color="red", fill=True)
sns.kdeplot(train_false["prediction"], label="FALSE", color="blue", fill=True)
plt.xlabel("Prediction")
plt.ylabel("Density")
plt.title("Density Plot of Predictions")
plt.legend(title="atRisk")
plt.show()

# Define threshold for vertical line
threshold = 0.02  # Replace with actual value

# Create the second density plot with vertical line
plt.figure(figsize=(8, 6))
sns.kdeplot(train_true["prediction"], label="TRUE", color="red", fill=True)
sns.kdeplot(train_false["prediction"], label="FALSE", color="blue", fill=True)
plt.axvline(x=threshold, color="blue", linestyle="dashed", label=f"Threshold = {threshold}")
plt.xlabel("Prediction")
plt.ylabel("Density")
plt.title("Density Plot of Predictions with Threshold")
plt.legend(title="atRisk")
plt.show()

Performance of Classifier

Confusion matrix

• The confusion matrix summarizes the classifier’s predictions against the actual known data categories.
  • Suppose the threshold is set as 0.02.

# Compute confusion matrix
dtest_1 = dtest_1.withColumn("predicted_class", when(col("prediction") > .02, 1).otherwise(0))
conf_matrix = dtest_1.groupBy("atRisk", "predicted_class").count().orderBy("atRisk", "predicted_class")

TP = dtest_1.filter((col("atRisk") == 1) & (col("predicted_class") == 1)).count()
FP = dtest_1.filter((col("atRisk") == 0) & (col("predicted_class") == 1)).count()
FN = dtest_1.filter((col("atRisk") == 1) & (col("predicted_class") == 0)).count()
TN = dtest_1.filter((col("atRisk") == 0) & (col("predicted_class") == 0)).count()

# Print formatted confusion matrix with labels
print("\n Confusion Matrix:\n")
print("                     Predicted")
print("            |  Negative  |  Positive  ")
print("------------+------------+------------")
print(f"Actual Neg. |    {TN:5}   |    {FP:5}  |")
print("------------+------------+------------")
print(f"Actual Pos. |    {FN:5}   |    {TP:5}  |")
print("------------+------------+------------")

Performance of Classifier

Accuracy

• Accuracy: When the classifier says this newborn baby is at risk or is not at risk, what is the probability that the model is correct?
  • Accuracy is defined as the number of items categorized correctly divided by the total number of items.

Performance of Classifier

False positive/negative

• False positive rate (FPR): If the classifier says this newborn baby is at risk, what’s the probability that the baby is not really at risk?
  • FPR is defined as the ratio of false positives to predicted positives.
• False negative rate (FNR): If the classifier says this newborn baby is not at risk, what’s the probability that the baby is really at risk?
  • FNR is defined as the ratio of false negatives to predicted negatives.

Performance of Classifier

Precision

• Precision: If the classifier says this newborn baby is at risk, what’s the probability that the baby is really at risk?
  • Precision is defined as the ratio of true positives to predicted positives.

Performance of Classifier

Recall (or Sensitivity)

• Recall (or sensitivity): Of all the babies at risk, what fraction did the classifier detect?
  • Recall (or sensitivity) is also called the true positive rate (TPR), the ratio of true positives over all actual positives.

Performance of Classifier

Specificity

• Specificity: Of all the not-at-risk babies, what fraction did the classifier detect?
  • Specificity is also called the true negative rate (TNR), the ratio of true negatives over all actual negatives.

Performance of Classifier

Enrichment

• Average: Average rate of new born babies being at risk
• Enrichment: How does the classifier precisely choose babies at risk relative to the average rate of new born babies being at risk?
  • We want a classifier whose enrichment is greater than 2.

accuracy = (TP + TN) / (TP + FP + FN + TN)
precision = TP / (TP + FP)
recall = TP / (TP + FN)
specificity = TN / (TN + FP)
average_rate = (TP + FN) / (TP + TN + FP + FN)  # Proportion of actual at-risk babies
enrichment = precision / average_rate

print(f"Accuracy:  {accuracy:.4f}")
print(f"Precision: {precision:.4f}")
print(f"Recall (Sensitivity): {recall:.4f}")
print(f"Specificity:  {specificity:.4f}")
print(f"Average Rate: {average_rate:.4f}")
print(f"Enrichment:   {enrichment:.4f} (Relative Precision)")

Performance of Classifier

Trade-off between recall and precision/enrichment

• There is a trade-off between recall and precision/enrichment.
  • What would be the optimal threshold?

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve

pdf = dtest_1.select("prediction", "atRisk").toPandas()

# Extract predictions and true labels
y_true = pdf["atRisk"]  # True labels
y_scores = pdf["prediction"]  # Predicted probabilities

# Compute precision, recall, and thresholds
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

# Compute enrichment: precision divided by average at-risk rate
average_rate = np.mean(y_true)
enrichment = precision / average_rate

# Define optimal threshold (example: threshold where recall ≈ enrichment balance)
optimal_threshold = 0.02  # Adjust based on the plot

# Plot Enrichment vs. Recall vs. Threshold
plt.figure(figsize=(8, 6))
plt.plot(thresholds, enrichment[:-1], label="Enrichment", color="blue", linestyle="--")
plt.plot(thresholds, recall[:-1], label="Recall", color="red", linestyle="-")

# Add vertical line for chosen threshold
plt.axvline(x=optimal_threshold, color="black", linestyle="dashed", label=f"Optimal Threshold = {optimal_threshold}")

# Labels and legend
plt.xlabel("Threshold")
plt.ylabel("Score")
plt.title("Enrichment vs. Recall")
plt.legend()
plt.grid(True)
plt.show()

Performance of Classifier

Trade-off between sensitivity and specificity

• There is also a trade-off between sensitivity and specificity.

• The receiver operating characteristic curve (or ROC curve) plot both the true positive rate (recall) and the false positive rate (or 1 - specificity) for all threshold levels.

  • Area under the curve (or AUC) can be another measure of the quality of the model.

from sklearn.metrics import roc_curve

# Convert to Pandas
pdf = dtest_1.select("prediction", "atRisk").toPandas()

# Compute ROC curve
fpr, tpr, _ = roc_curve(pdf["atRisk"], pdf["prediction"])

# Plot ROC curve
plt.figure(figsize=(8,6))
plt.plot(fpr, tpr, label=f"ROC Curve (AUC = {auc:.4f})")
plt.plot([0, 1], [0, 1], 'k--', label="Random Guess")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("ROC Curve")
plt.legend()
plt.show()

Performance of Classifier

AUC

• (0,0)—Corresponding to a classifier defined by the threshold \(\text{Prob}(y_{i} = 1) = 1\):
  • Nothing gets classified as at-risk.

Performance of Classifier

AUC

• (1,1)—Corresponding to a classifier defined by the threshold \(\text{Prob}(y_{i} = 1) = 0\):
  • Everything gets classified as at-risk.

Performance of Classifier

AUC

• (0,1)—Corresponding to any classifier defined by a threshold between 0 and 1:
  • Everything is classified perfectly!

Performance of Classifier

AUC

• The AUC for the random model is 0.5.

  • You want a classifier whose AUC is close to 1, and greater than 0.5.

• When comparing multiple classifiers, you generally want to prefer classifiers that have a higher AUC.

• You also want to examine the shape of the ROC to explore possible trade-offs.

Performance of Classifier

• Suppose that you have successfully trained a classifier with acceptable precision and recall using NY hospital data.
• Now you want to apply the same classifier on all hospital data in MA.
  • Will the classifier perform as well?
• The proportion of at-risk babies in MA hospitals may differ from that in NY.
  • Can this difference impact classifier performance on MA data?
• Let’s examine how classifier performance changes with varying at-risk rates.

dtrain, dtest = df.randomSplit([0.5, 0.5], seed = 1234)

pd_dtrain = dtrain.toPandas()
pd_dtest = dtest.toPandas()

# Set seed for reproducibility
np.random.seed(23464)

# Sample 1000 random indices from the test dataset without replacement
sample_indices = np.random.choice(pd_dtest.index, size=1000, replace=False)

# Separate the selected observations from testing data
separated = pd_dtest.loc[sample_indices]

# Remove the selected observations from the testing data
# Consider this as data from NY hospitals
pd_dtest_NY = pd_dtest.drop(sample_indices)

# Split the separated sample into at-risk and not-at-risk groups
at_risk_sample = separated[separated["atRisk"] == 1]  # Only at-risk cases
not_at_risk_sample = separated[separated["atRisk"] == 0]  # Only not-at-risk cases

# Create test sets for MA hospitals with different at-risk rates
pd_dtest_MA_moreRisk = pd.concat([pd_dtest_NY, at_risk_sample])  # Adds back only at-risk cases
pd_dtest_MA_lessRisk = pd.concat([pd_dtest_NY, not_at_risk_sample])  # Adds back only not-at-risk cases

# Show counts to verify results
print("Original Test Set Size:", pd_dtest.shape[0])
print("Sampled Separated Size:", separated.shape[0])
print("NY Hospitals Data Size:", pd_dtest_NY.shape[0])
print("MA More Risk Data Size:", pd_dtest_MA_moreRisk.shape[0])
print("MA Less Risk Data Size:", pd_dtest_MA_lessRisk.shape[0])

Performance of Classifier

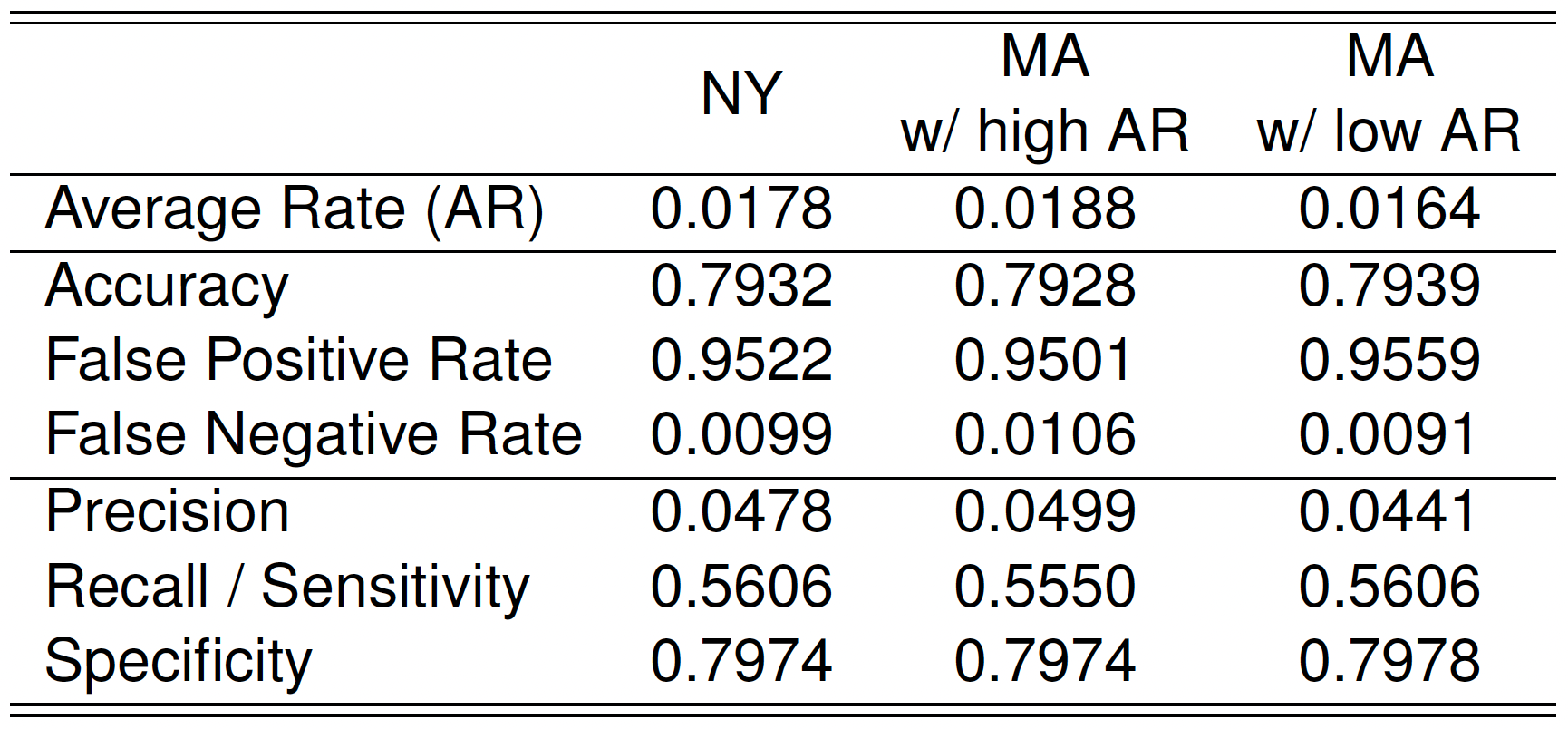
Performance of Classifier

• Which classifier do you prefer for identifying at-risk babies?
  1. High accuracy, low recall, other things being equal;
  2. Low accuracy, high recall, other things being equal.
• Accuracy may not be a good measure for the classes that have unbalanced distribution of predicted probabilities (e.g., rare event).

Accuracy Can Be Misleading in Imbalanced Data

• Rare events (e.g., severe childbirth complications) occur in a very small percentage of cases (e.g., 1% of the population).
• A simple model that always predicts “not-at-risk” would be 99% accurate, as it correctly classifies 99% of cases where no complications occur.
• However, this does not mean the simple model is better—accuracy alone does not capture the effectiveness of a model when class distributions are skewed.
• A better model that identifies 5% of cases as “at-risk” and catches all true at-risk cases may appear to have lower overall accuracy than the simple model.
• Missing a severe complication (false negative) can be more costly than mistakenly flagging a healthy case as at risk (false positive).

Separation and Quasi-separation

What is Separation?

• One of the model variables or some combination of the model variables predicts the outcome perfectly for at least a subset of the training data.
  • You’d think this would be a good thing; but, ironically, logistic regression fails when the variables are too powerful.
• Separation occurs when a predictor (or combination of predictors) perfectly separates the outcome classes.
• For example, if:
  • All fail = TRUE when safety = low, and
  • All fail = FALSE when safety ≠ low,
    then the model can predict the outcome with 100% accuracy based on safety.

➡️ This leads to infinite (non-estimable) coefficients and convergence problems.

What is Quasi-Separation?

• Quasi-separation occurs when:
  • Some, but not all, values of a predictor perfectly predict the outcome.
• Example:
  • fail = TRUE for all cars with safety = low,
    
  • But fail is mixed for safety = med or high.

➡️ Model still suffers from unstable coefficient estimates or high standard errors.

Example of Quasi-separation

• Suppose a car review site rates cars on several characteristics, including affordability and safety rating.
• Car ratings can be “very good,” “good,” “acceptable,” or “unacceptable.”
• Your goal is to predict whether a car will fail the review: that is, get an unacceptable rating.
  • Let’s do Classwork 11.