Midterm Exam II

Version B

Published

November 19, 2025

Section 1. Multiple Choice

Question 1

Which of the following is NOT listed as a key characteristic of a Data Warehouse?

  1. It integrates data from multiple sources (internal and external).
  2. It is designed primarily for real-time transaction processing.
  3. It is schema-based, requiring data to fit a predefined structure.
  4. It often includes 5+ years of historical, archived data.

Answer: b

A data warehouse is designed mainly for analytics and historical querying, not for real-time transaction processing.


Question 2

When the distribution of a variable has a single peak and is positively skewed (i.e., having a long right tail), which of the following is correct?

  1. Median = Mean = Mode
  2. Median < Mode < Mean
  3. Mean < Median < Mode
  4. Mode < Median < Mean

Answer: d

For a positively skewed distribution (long right tail), the order is:
Mode (at the peak) < Median < Mean (pulled right by large values).


Question 3

What is NOT an essential component in ggplot() data visualization?

  1. Data frames
  2. Geometric objects
  3. Facets
  4. Aesthetic attributes

Answer: c

Facets are useful but optional. You can build a valid ggplot without them.


Question 4

____(1)____ does not necessarily imply ____(2)____

    1. Correlation; (2) causation
    1. Causation; (2) correlation
    1. Correlation; (2) correlation
    1. Causation; (2) causation

Answer: a

The classic warning: correlation does not imply causation.


Question 5

In the context of the lecture, which of the following correctly interprets a change in log-transformed GDP per capita and its meaning for GDP per capita?

  1. A 0.01 increase in log(GDP per capita) corresponds to a 1% increase in GDP per capita.
  2. A 1-unit increase in log(GDP per capita) corresponds to a 1% increase in GDP per capita.
  3. A one-unit increase in GDP per capita means an 8.4% increase in GDP per capita.
  4. Both (a) and (c) are correct.

Answer: a

For small changes, a change of 0.01 in log(GDP per capita) is approximately a 1% change in GDP per capita.


Question 6

Which “V” of Big Data is most directly about whether the data is accurate and trustworthy?

  1. Value
  2. Velocity
  3. Variety
  4. Veracity

Answer: d

Veracity is about data quality, accuracy, and trustworthiness.



Section 2. Filling-in-the-Blanks

Question 7

____________________ describes how the values of a variable are spread or grouped within a dataset, while ____________________ is the tendency of a variable’s values to differ from one measurement to another.

First blank: distribution
Second blank: variability


Question 8

In the context of time trend analysis, a fitted curve is often added to a line chart to help smooth out ____________________ to reveal the overall pattern.

short-term fluctuations


Question 9

The gg in ggplot stands for ____________________.

Grammar of Graphics


Question 10

Using ____________________—a machine learning method—the geom_smooth() visualizes the ____________________ value of the y variable for a given value of the x variable. The grey ribbon around the curve illustrates the ____________________ surrounding the estimated curve.

Using regression — a machine learning method — the geom_smooth() visualizes the predicted value of the y variable for a given value of the x variable. The grey ribbon around the curve illustrates the uncertainty surrounding the estimated curve.


Question 11

When observing a histogram, if the distribution has two distinct peaks, it is described as ____________________; whereas a distribution where values are relatively equal across the range is described as ____________________.

First blank: bimodal
Second blank: uniform


Question 12

When visualizing the distribution of a single numerical variable using geom_histogram(), you must choose between specifying the number of ____________________ or the ____________________ of the intervals. You cannot specify both simultaneously.

First blank: bins
Second blank: width



Section 3. Data Transformation and Visualization with R

Questions 13-19

For Questions 13-19, consider the following R packages and the data.frame, nwsl_player_stats, containing individual player statistics for the National Women’s Soccer League (NWSL) in the 2022 season:

library(tidyverse)
library(skimr)
nwsl_player_stats <- read_csv("https://bcdanl.github.io/data/nwsl_player_stats.csv")
  • The nwsl_player_stats data.frame is with 314 observations and 13 variables.
  • The first 5 observations in the nwsl_player_stats data.frame are displayed below:
player nation pos squad age mp starts min
M. A. Vignola us USA MFFW Angel City 23 2 0 18
Michaela Abam cm CMR FW Dash 24 12 3 273
Kerry Abello us USA FWMF Pride 22 21 12 1042
Jillienne Aguilera NA DFMF Red Stars NA 17 5 580
Tinaya Alexander eng ENG FWMF Spirit 22 9 1 167
player nation pos squad xGp90 xAp90 xGxAp90
M. A. Vignola us USA MFFW Angel City 0.00 0.00 0.00
Michaela Abam cm CMR FW Dash 0.26 0.10 0.36
Kerry Abello us USA FWMF Pride 0.16 0.05 0.20
Jillienne Aguilera NA DFMF Red Stars 0.05 0.04 0.09
Tinaya Alexander eng ENG FWMF Spirit 0.58 0.03 0.62
player nation pos squad npxGp90 npxGxAp90
M. A. Vignola us USA MFFW Angel City 0.00 0.00
Michaela Abam cm CMR FW Dash 0.26 0.36
Kerry Abello us USA FWMF Pride 0.16 0.20
Jillienne Aguilera NA DFMF Red Stars 0.05 0.09
Tinaya Alexander eng ENG FWMF Spirit 0.16 0.19

Description of Variables in nwsl_player_stats:

  • player: Player name

  • nation: Player home country

  • pos: Player position (e.g., GK, FW, MF, etc.)

  • squad: Player team

  • age: Age of player

  • mp: Matches played

  • starts: Number of matches in which player started the game

  • min: Total minutes played in the season

  • xGp90: Expected goals per ninety minutes

    • xG is simply the probability of scoring a goal from a given spot on the field when a shot is taken.

  • xAp90: Expected assists per ninety minutes

    • xA is simply the probability of assisting a goal by delivering a pass that creates a scoring opportunity.

  • xGxAp90: Expected goals plus assists per ninety minutes

  • npxGp90: Expected goals minus penalty goals per ninety minutes

  • npxGxAp90: Expected goals plus assists minus penalty goals per ninety minutes

A player who is consistently achieving a high number of xG (or xA) will be one who is getting into a good position consistently on the field. Coaches and scouts can use this to evaluate whether a player is exceedingly (un)lucky over a given number of games, and this will help in evaluating that player’s offensive skills beyond simple counts.


The followings are the summary of the nwsl_player_stats data.frame, including descriptive statistics for each variable.

Data summary
Name nwsl_player_stats
Number of rows 314
Number of columns 13
_______________________
Column type frequency:
character 4
numeric 9
________________________
Group variables None

Variable type: character

skim_variable n_missing min max empty n_unique
player 0 5 26 0 303
nation 17 6 7 0 29
pos 0 2 4 0 10
squad 0 4 10 0 12

Variable type: numeric

skim_variable n_missing mean sd p0 p25 p50 p75 p100
age 15 25.98 3.96 16 23.00 25.00 28.00 38.00
mp 0 12.61 6.95 1 6.00 14.00 19.00 22.00
starts 0 9.25 7.31 0 2.00 9.00 16.00 22.00
min 0 831.81 631.52 1 234.00 743.50 1398.00 1980.00
xGp90 2 0.13 0.16 0 0.01 0.06 0.20 0.77
xAp90 2 0.10 0.47 0 0.01 0.05 0.11 8.26
xGxAp90 2 0.23 0.50 0 0.04 0.13 0.32 8.26
npxGp90 2 0.12 0.14 0 0.01 0.06 0.18 0.77
npxGxAp90 2 0.22 0.50 0 0.04 0.13 0.30 8.26

Question 13

Write a code to produce the above summary for the nwsl_player_stats data.frame, including descriptive statistics for each variable.

Answer: ______________________________________________

skim(nwsl_player_stats)


Question 14

What code would you use to count the number of players in each team?

  1. nwsl_player_stats |> count(player)
  2. nwsl_player_stats |> count(nation)
  3. nwsl_player_stats |> count(pos)
  4. nwsl_player_stats |> count(squad)

d


Question 15

What is the median value of starts? Find this value from the summary of the nwsl_player_stats data.frame.

Answer: ______________________________________________

9


Question 16

  • We are interested in players who score or assist on a goal.
  • To achieve this, we create a new data.frame, a new data.frame, nwsl_nonGK_stats, which includes only players who are NOT a goal keeper from the nwsl_player_stats data.frame.
nwsl_nonGK_stats <- nwsl_player_stats |> 
  filter(___BLANK___)
  • The pos value is “GK” for a goal keeper. Which condition correctly fills in the BLANK to complete the code above?
  1. !is.na(pos)
  2. is.na(pos)
  3. pos != "GK"
  4. pos == "GK"
  5. Both a and c
  6. Both b and d

c


Question 17

  • Additionally, we are interested in non-goalkeeper players who played matches consistently throughout the season.
  • To achieve this, we create a new data.frame, nwsl_nonGK_stats_filtered, which includes only non GK players who played in at least 10 matches (mp) and started in at least 7 matches (starts) .
nwsl_nonGK_stats_filtered <- nwsl_nonGK_stats |> 
  filter(___BLANK___)
  • Which condition correctly fills in the BLANK to complete the code above?
  1. mp > 10 | starts > 7
  2. mp >= 10 | starts >= 7
  3. mp > 10 & starts > 7
  4. mp >= 10 & starts >= 7

d

We want players who meet both conditions: played in at least 10 matches (mp >= 10) and started in at least 7 matches (starts >= 7). The logical operator & ensures both conditions are met.


Question 18

How would you describe the relationship between age and xGp90 (expected goals per ninety minutes) using the nwsl_nonGK_stats_filtered data.frame?

  • To identify outlier players, such as star players and young players, some player names are added to such points in the plot.
  • Note that it is NOT required to provide the code for adding these texts to the plot.

Complete the code by filling in the blanks (1)-(4).

ggplot(data = ___(1)___,
       mapping = aes(x = ___(2)___, 
                     y = ___(3)___)) +
  geom_point(alpha = 0.5) +
  ___(4)___()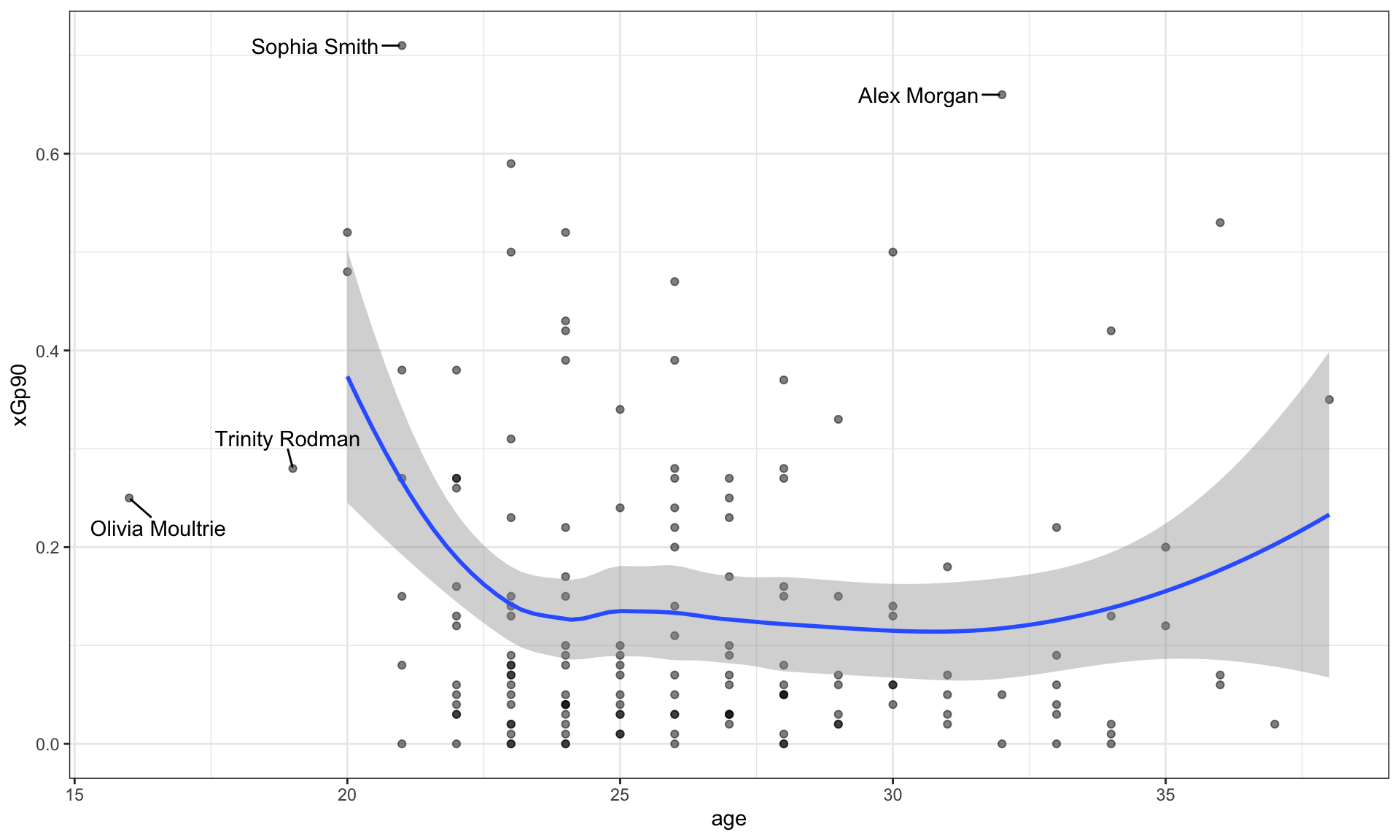

Blank (1)

  1. nwsl_nonGK_stats_filtered
  2. nwsl_nonGK_stats
  3. nwsl_player_stats

a


Blank (2)

  1. age
  2. xGxAp90
  3. xGp90
  4. xAp90

a


Blank (3)

  1. age
  2. xGxAp90
  3. xGp90
  4. xAp90

c


Blank (4)

  1. geom_fit
  2. geom_scatterplot
  3. geom_smooth
  4. geom_histogram

c


Young Players

Who are the young players under the age of 20 in the given plot?

Answer: ______________________________________________

Olivia Moultrie and Trinity Rodman


Star Players

Who are the star players whose xGp90 is greater than 0.6 in the given plot?

Answer: ______________________________________________

Sophia Smith and Alex Morgan


Relationship

Describe the overall relationship between age and xGp90 (expected goal per ninety minutes).

Overall, xGp90 decreases as age increases up to about 24, after which it levels off and remains relatively constant.

This suggests that younger players tend to experience a steeper decline in xGp90 with age early on, while changes become much smaller after the mid-20s.


Question 19

How would you describe how the distribution of xAp90 (expected assist per ninety minutes) varies by teams (squad) using the nwsl_nonGK_stats_filtered data.frame?

  • Note that the squad categories are sorted by the median of xAp90 in the plot.

Complete the code by filling in the blanks.

ggplot(data = ___(1)___,
       mapping = aes(___(2)___, 
                     y = ___(3)___)) +
  ___(4)___() +
  labs(y = "NWSL Teams")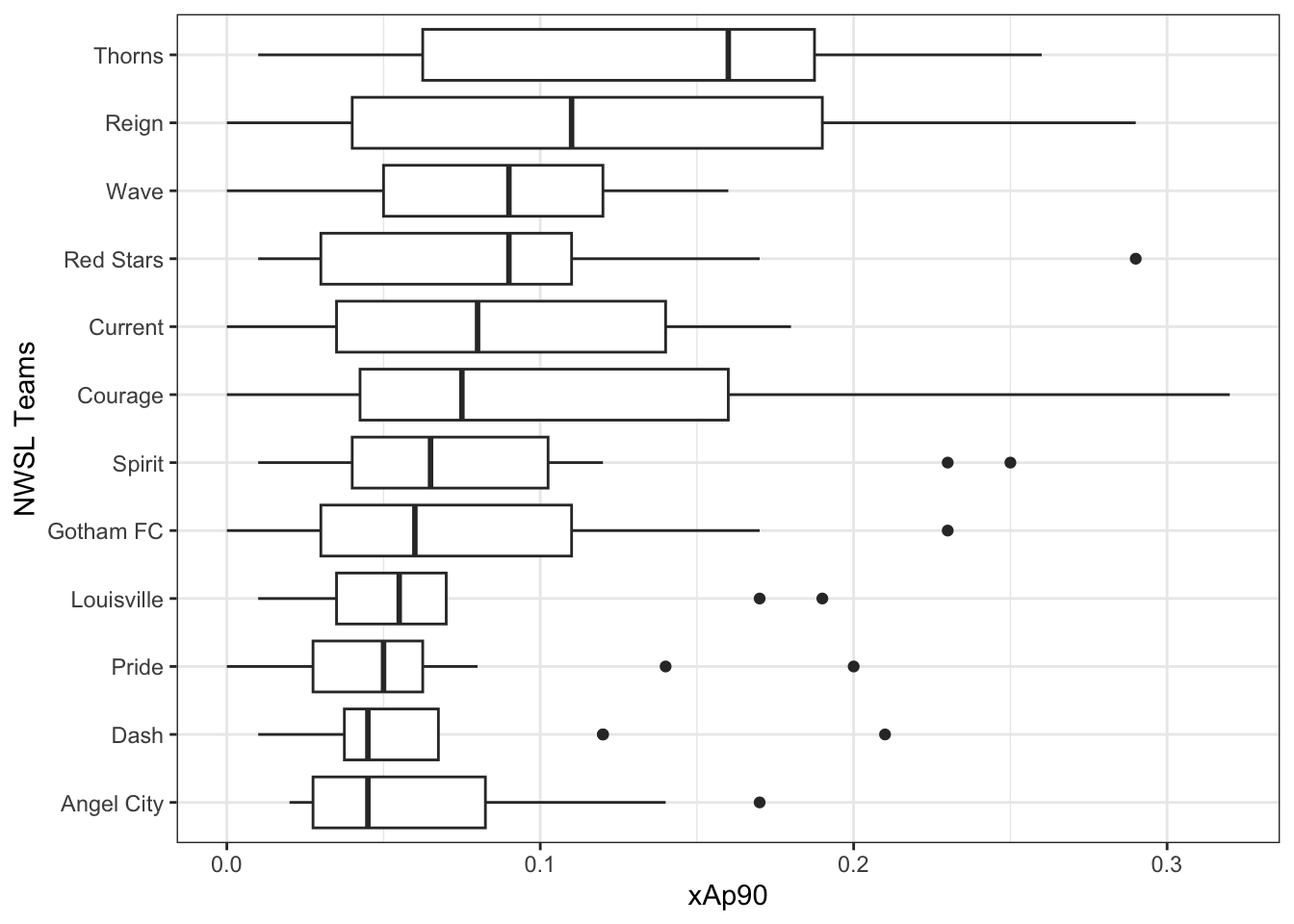

Blank (1)

  1. nwsl_nonGK_stats_filtered
  2. nwsl_nonGK_stats
  3. nwsl_player_stats

a


Blank (2)

  1. x = squad
  2. y = squad
  3. x = xGxAp90
  4. y = xGxAp90
  5. x = xGp90
  6. y = xGp90
  7. x = xAp90
  8. y = xAp90

g


Blank (3)

  1. fct_reorder(squad, xAp90)
  2. fct_reorder(xAp90, squad)
  3. fct_reorder(squad, xGp90)
  4. fct_reorder(xGp90, squad)
  5. fct_reorder(squad, xGxAp90)
  6. fct_reorder(xGxAp90, squad)

a


Blank (4)

  1. geom_bar
  2. geom_box
  3. geom_boxplot
  4. geom_histogram

c



Question 20

For Question 20, you will use the following R packages and a data.frame named chess_top4, which contains information about chess games played by four of the world’s top online chess players during a special event called “Titled Tuesday” on chess.com. These games were played in a format where each player has 3 minutes to make all their moves, with 1 second added to their clock after each move. The data includes games from October 2022 to October 2024 played only among the following four players:

  1. Magnus Carlsen
  2. Hikaru Nakamura
  3. Alireza Firouzja
  4. Daniel Naroditsky

Note: Titled Tuesday is a weekly event held every Tuesday on chess.com, where titled chess players (such as Grandmasters and International Masters) compete in online tournaments.

library(tidyverse)
chess_top4 <- read_csv("https://bcdanl.github.io/data/chess_titled_tuesday.csv")

The first 15 observations in the chess_top4 data.frame are displayed below:

Date White Black Result
2022-10-11 Hikaru Nakamura Magnus Carlsen White Wins
2022-10-18 Hikaru Nakamura Alireza Firouzja Draw
2022-10-25 Daniel Naroditsky Alireza Firouzja Draw
2022-11-08 Hikaru Nakamura Alireza Firouzja Black Wins
2022-12-13 Alireza Firouzja Hikaru Nakamura Draw
2022-12-20 Hikaru Nakamura Alireza Firouzja White Wins
2022-12-20 Magnus Carlsen Hikaru Nakamura Draw
2023-01-03 Daniel Naroditsky Hikaru Nakamura Black Wins
2023-01-03 Hikaru Nakamura Magnus Carlsen White Wins
2023-01-24 Hikaru Nakamura Magnus Carlsen White Wins
2023-02-28 Alireza Firouzja Magnus Carlsen Draw
2023-02-28 Hikaru Nakamura Alireza Firouzja Draw
2023-02-28 Hikaru Nakamura Magnus Carlsen Draw
2023-02-28 Magnus Carlsen Hikaru Nakamura Draw
2023-03-14 Hikaru Nakamura Alireza Firouzja White Wins
  • The chess_top4 data.frame contains 70 observations and 4 variables, representing 70 unique chess games.

Description of Variables in chess_top4:

  • Date: The date when the game was played.

  • White: The name of the player who played with the white pieces.

  • Black: The name of the player who played with the black pieces.

  • Result: The outcome of the game, which can be one of the following:

    • “White Wins” (the player with the white pieces won the game)
    • “Black Wins” (the player with the black pieces won the game)
    • “Draw” (the game ended in a tie)

Question 20 is about a ggplot code to visualize how the distribution of Result varies among these top 4 chess players.

Part 1

Complete the code by filling in the blanks to replicate the given plot.

  • The White player is displayed on the vertical axis.
  • The Black player is labeled at the top of each panel.
ggplot(data = chess_top4,
       mapping = aes(___(1)___,
                     fill = ___(2)___)) +
  geom_bar(___(3)___) +
  facet_wrap(___(4)___, ncol = 1) +
  labs(x = "Proportion")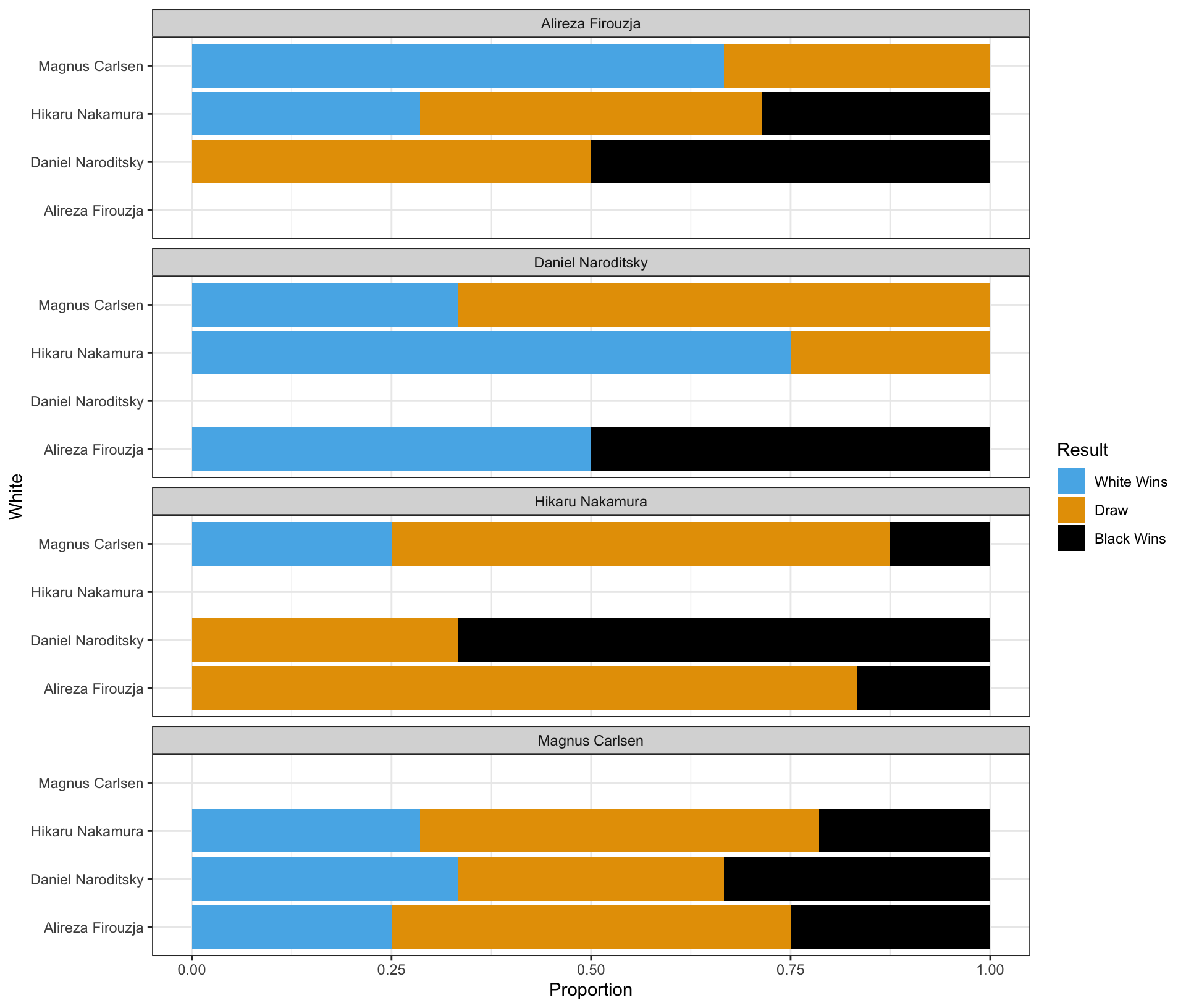

Blank (1)
  1. x = White
  2. y = White
  3. x = Black
  4. y = Black
  5. x = Proportion
  6. y = Proportion

b


Blank (2)
  1. chess_top4
  2. White
  3. Black
  4. Result
  5. count

d


Blank (3)
  1. position = "stack"
  2. position = "fill"
  3. position = "dodge"
  4. Leaving (3) empty
  5. Both a and d
  6. Both b and d
  7. Both c and d

b


Blank (4)
  1. White
  2. ~White
  3. Black
  4. ~Black
  5. Player
  6. ~Player
  7. both a and b
  8. both c and d
  9. both e and f
  10. both b and f
  11. both d and f

d


Part 2

Complete the code by filling in the blanks to replicate the given plot.

  • The White player is displayed on the vertical axis.
  • The Black player is labeled at the top of each panel.
ggplot(data = chess_top4,
       mapping = aes(___(1)___,
                     fill = ___(2)___)) +
  geom_bar(___(3)___) +
  facet_wrap(___(4)___, ncol = 1)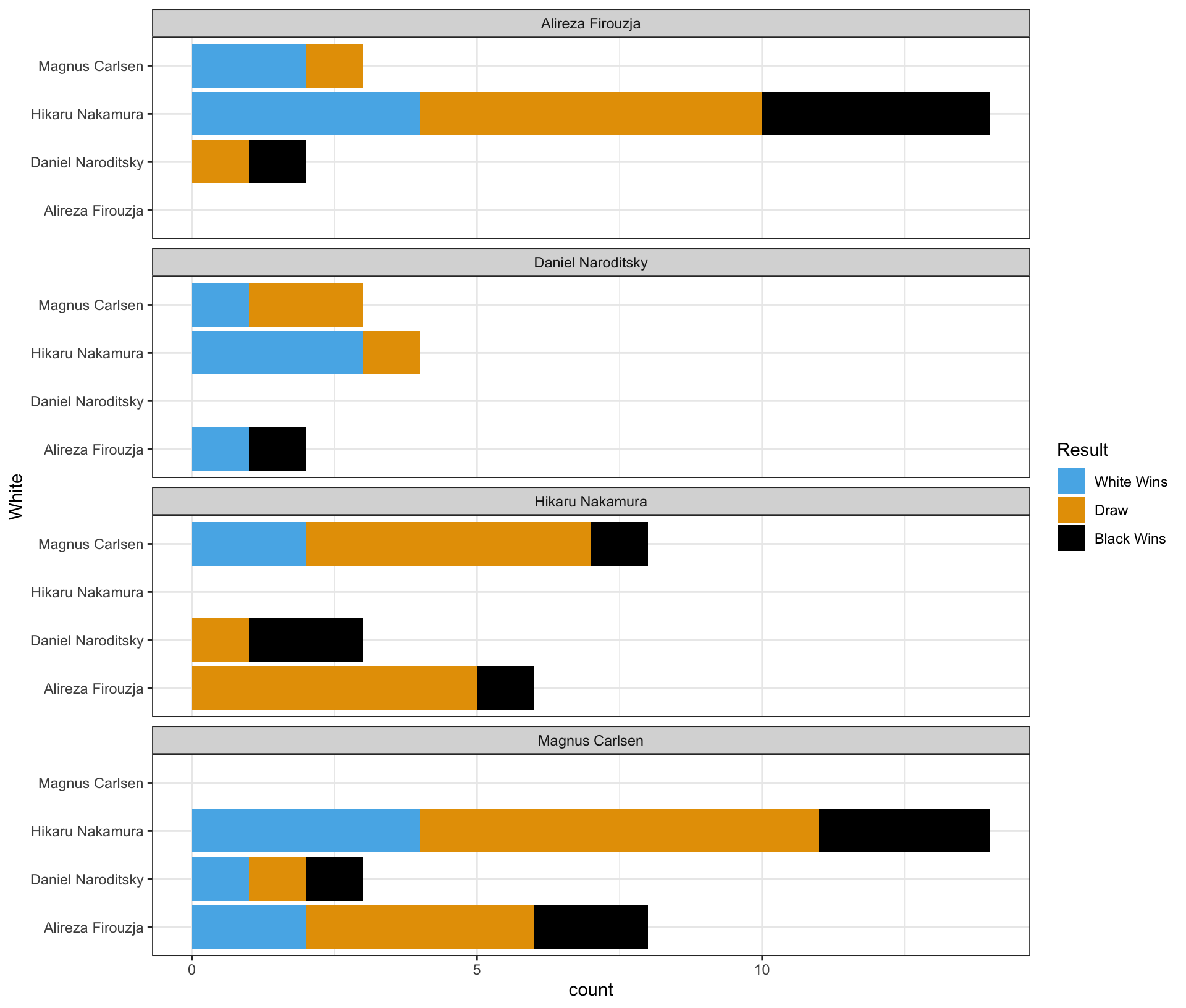

Blank (1)
  1. x = White
  2. y = White
  3. x = Black
  4. y = Black
  5. x = count
  6. y = count

b


Blank (2)
  1. chess_top4
  2. White
  3. Black
  4. Result
  5. count

d


Blank (3)
  1. position = "stack"
  2. position = "fill"
  3. position = "dodge"
  4. Leaving (3) empty
  5. Both a and d
  6. Both b and d
  7. Both c and d

e


Blank (4)
  1. White
  2. ~White
  3. Black
  4. ~Black
  5. Player
  6. ~Player
  7. both a and b
  8. both c and d
  9. both e and f
  10. both b and f
  11. both d and f

d


Part 3

Complete the code by filling in the blanks to replicate the given plot.

  • The White player is displayed on the vertical axis.
  • The Black player is labeled at the top of each panel.
ggplot(data = chess_top4,
       mapping = aes(___(1)___,
                     fill = ___(2)___)) +
  geom_bar(___(3)___) +
  facet_wrap(___(4)___, ncol = 1)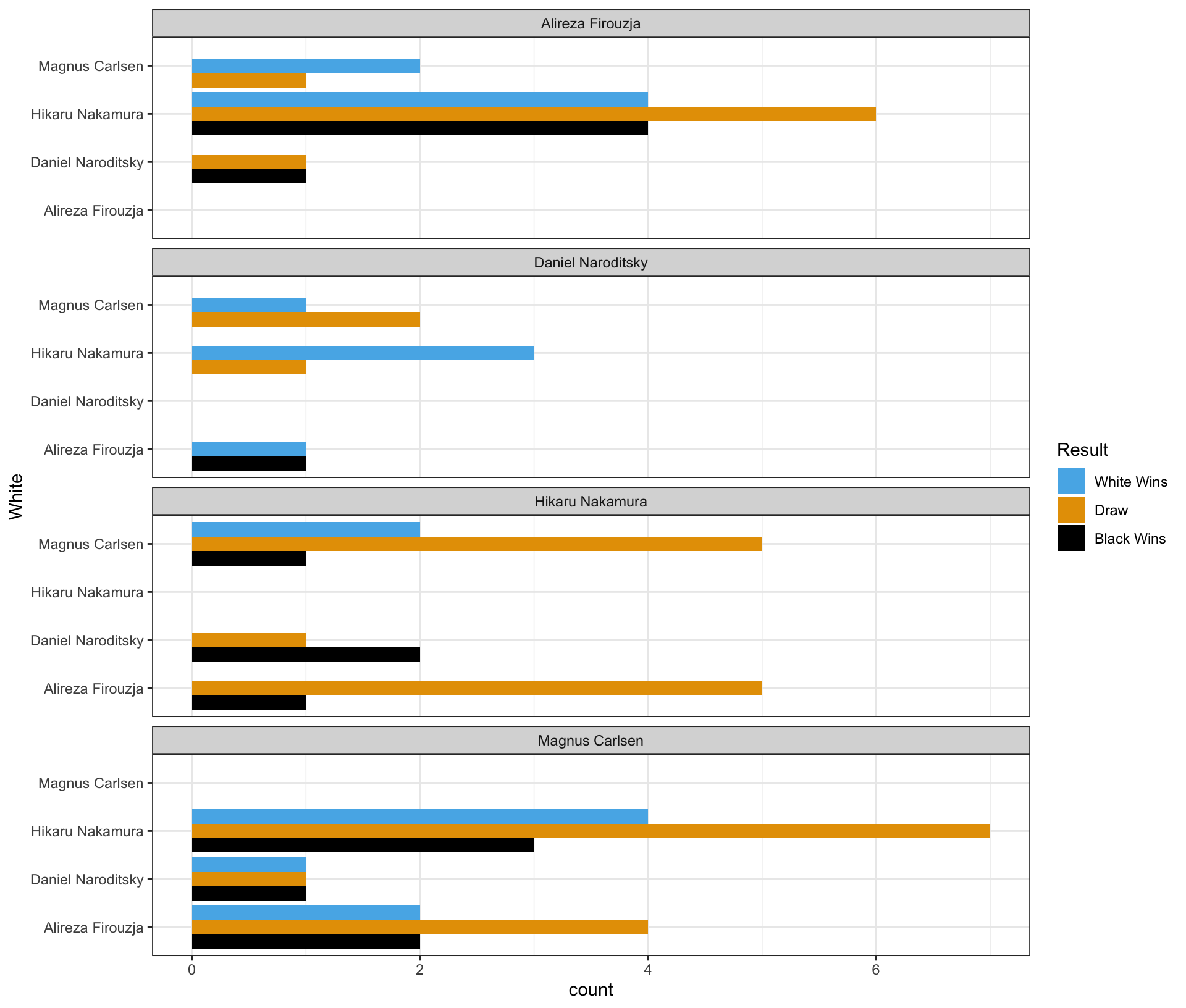

Blank (1)
  1. x = White
  2. y = White
  3. x = Black
  4. y = Black
  5. x = count
  6. y = count

b


Blank (2)
  1. chess_top4
  2. White
  3. Black
  4. Result
  5. count

d


Blank (3)
  1. position = "stack"
  2. position = "fill"
  3. position = "dodge"
  4. Leaving (3) empty
  5. Both a and d
  6. Both b and d
  7. Both c and d

c


Blank (4)
  1. White
  2. ~White
  3. Black
  4. ~Black
  5. Player
  6. ~Player
  7. both a and b
  8. both c and d
  9. both e and f
  10. both b and f
  11. both d and f

d


Part 4 - Magnus Carlsen vs. Hikaru Nakamura in the Titled Tuesday

Who had more wins in the games where Magnus Carlsen played with the white pieces and Hikaru Nakamura played with the black pieces in the Titled Tuesday?

Answer: ______________________________________________

Magnus Carlsen


Who had more wins in the games where Hikaru Nakamura played with the white pieces and Magnus Carlsen played with the black pieces in the Titled Tuesday?

Answer: ______________________________________________

Hikaru Nakamura


Who won more games in the encounters between Magnus Carlsen and Hikaru Nakamura in the Titled Tuesday?

Answer: ______________________________________________

They had an equal number of wins.


Section 3. Short Essay

Question 21

What are the advantage and disadvantage of using the scales option in ggplot2 when creating faceted plots?

  • Advantages:
    • Customized Scales per Facet: Using scales = "free" (or "free_x", "free_y") allows each facet to have its own axis scales. This can make patterns within each facet more visible, especially when the data ranges vary significantly between facets.
  • Disadvantages:
    • Difficulty in Comparison: When scales are free, comparing values across facets becomes challenging because the axes are not standardized. Viewers might misinterpret the data, thinking that similar bar heights represent similar values, even if the scales differ.


Question 22

How does data storytelling bridge the gap between data and insights?

Data Storytelling bridges the gap between data and insight by integrating descriptive statistics, data transformation, visualization, and narration within the appropriate audience context to communicate findings effectively and support data-informed decision-making.


Question 23

Provide two main reasons why the log transformation of a variable can be useful.

Two main reasons for using a log transformation are:

  1. It helps reduce skewness in highly right-skewed data, making the distribution more symmetric and the variation easier to see.
  2. It allows us to interpret changes in percentage terms, which is especially useful for growth rates and economic variables such as income, GDP, stock price, or housing price.


Question 24

Provide at least three techniques to make data visualization more colorblind-friendly.

To make visualizations more accessible and colorblind-friendly, consider:

  1. Using colorblind-friendly color palettes
  2. Adding non-color cues like shape to scatterplots or linetype to line charts
  3. Including additional visual cues to highlight important information (e.g., annotations or labels)
  4. Ensuring strong contrast between colors and between the foreground and background so that elements remain distinguishable.


Question 25

For each of the workplaces represented by our three alumni guest speakers, explain how generative AI is used in their day-to-day work.

Across the three alumni workplaces, generative AI is integrated into daily workflows in different but complementary ways.

At the analytics and engineering–focused workplace, many employees (roughly 60–80%) use AI assistants such as Copilot or Claude to support coding, debugging, and data processing. AI significantly speeds up routine analytical tasks, but all outputs still require human review, meaning AI augments rather than replaces analysts.

For a traditional data analyst role, generative AI is commonly used to assist with SQL coding, data summarization, and report drafting. Analysts rely on AI to improve efficiency, but data sensitivity and responsible AI use are essential, so such tools are typically deployed only within secure internal environments.

At the policy and government-related workplace (e.g., the Federal Reserve), the use of public AI tools like ChatGPT is prohibited due to strict data confidentiality rules. Instead, analysts rely on approved internal systems and traditional analytical tools to protect sensitive economic and financial information.

Together, these examples show how generative AI is widely used to increase productivity, while security, privacy, and human oversight remain central across all workplaces.


Back to top